Dao's Archimedean Twins - Second Pair

Problem

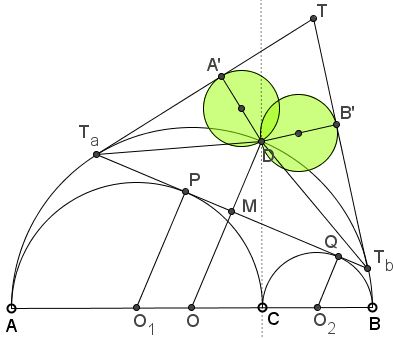
Consider an arbelos formed by semicircles $(O_{1}),$ $(O_{2}),$ and $(O)$ of radii $a,$ $b,$ and $a + b.$ The famous Archimedean twin circles in an arbelos have equal radii $\displaystyle\frac{ab}{a+b}.$

Let $CD$ be the common tangent line $(O_{1})$ and $(O_{2}),$ and extend their other common tangent $PQ$ to intersect $(O)$ at $T_a$ and $T_b.$

Let $A'$ and $B'$ be the orthogonal projections of $D$ on the tangents to $(O)$ at $T_a$ and $T_b,$ respectively.

Dao's Archimedean Twins - Second Pair, construction

The circles with diameters $DA'$ and $DB'$ are congruent to the Archimedean twins.

Proof

Point $D$ happens to be the midpoint of arc $T_{a}T_{b}$ (and the fourth vertex of the parallelogram $PCQD)$. This makes $(O{2}P,$ $OD,$ and $O_{2}Q$ parallel. Next, since $O_{1}O_{2}=a+b,$ we find that $OO_{2} = a=O_{2}P$ and $OO_{1}=b=O_{2}Q.$ Further, if $M$ is the intersection of $OD$ and $T_{a}T_b,$ then

Dao's Archimedean Twins - Second Pair, Proof 1

$\displaystyle OM=\frac{a}{a+b}O_{1}P+\frac{b}{a+b}O_{2}Q=\frac{a^{2}+b^{2}}{a+b}.$

It follows that

$\displaystyle DM=(a+b)-\frac{a^{2}+b^{2}}{a+b}=\frac{2ab}{a+b}.$

such that the circle with diameter DM is Archimedean (this was known earlier.)

Turning to angles, let $T$ be the intersection of the two tangents. Observe that $\angle T_{b}T_{a}D$ is half the $\angle T_{b}T_{a}T$. Similarly, $\angle T_{a}T_{b}D=\frac{1}{2}\angle T_{a}T_{b}T.$ It follows that $D$ is the incenter of $\Delta T_{a}T_{b}T,$ making $DT_{a}=DT_{b}=DM$ and implying that the circles on $DT_{a}$ and $DT_{b}$ are also Archimedean.

Acknowledgment

The discovery of this pair of Archimedean twins and the proof are due to Dao Thanh Oai. The proof has been published in Forum Geometricorum.

71536475