From Arbitrary Pentagon to Regular One
What Might This Be About?
Problem
Let $A_0A_1A_2A_3A_4$ be an arbitrary pentagon. For $i=0,\ldots,4,$ form linear combinations (where indices are taken modulo $5)$:
$\displaystyle B_{i}=\frac{A_{i}+\phi A_{i+1}+A_{i+2}}{2+\phi}.$
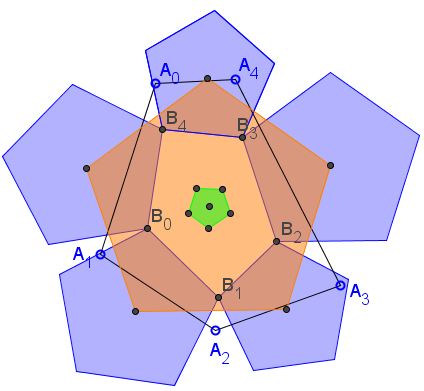
Then the centers of regular polygons erected either internally or externally on the sides of $B_{0}B_{1}B_{2}B_{3}B_{4}$ form a regular pentagon.
Solution
We shall use complex numbers and identify them with the points in the plane. The proof is based on the assertion that all four pentagons involved - $A_0A_1A_2A_3A_4,$ $B_{0}B_{1}B_{2}B_{3}B_{4},$ and the two allegedly regular ones - have the same barycenter.
This is easily seen for the first two:
$\begin{align}\displaystyle \frac{1}{5}\sum_{k=0}^{4}B_{k} &= \frac{1}{5(2+\phi )}\sum_{k=0}^{4}(A_{k}+\phi A_{k+1}+A_{k+2})\\ &= \frac{1}{5(2+\phi )}\bigg(\sum_{k=0}^{4}A_{k}+\phi\sum_{k=0}^{4}A_{k+1}+\sum_{k=0}^{4}A_{k+2}\bigg)\\ &= \frac{1}{5(2+\phi )}\bigg(\sum_{k=0}^{4}A_{k}+\phi\sum_{k=0}^{4}A_{k}+\sum_{k=0}^{4}A_{k}\bigg)\\ &= \frac{1}{5(2+\phi )}(2+\phi )\sum_{k=0}^{4}A_{k}\\ &= \frac{1}{5}\sum_{k=0}^{4}A_{k}. \end{align}$
The same derivation works for any polygon obtained from $A_0A_1A_2A_3A_4$ by a linear polygonal transformation, of which $B_{0}B_{1}B_{2}B_{3}B_{4}$ is one example. It will be seen that this is how the two allegedly regular polygons are obtained from $B_{0}B_{1}B_{2}B_{3}B_{4}.$
It is convenient to assume that $A_0A_1A_2A_3A_4$ and $B_{0}B_{1}B_{2}B_{3}B_{4}$ have the origin as the barycenter by this convention, $\displaystyle\sum_{k=0}^{4}A_{k}=0.$
Given two points $X$ and $Y,$ there are two regular pentagons that have $XY$ as one of the sides. The centers of these pentagons can be found as
$Q=(1-\tau )X+\tau Y,$
where $\displaystyle \tau=\frac{1}{2}(1\pm i\cdot \tan 54^{\circ}).$ In what follows I'll use the sign $+$ since the other case may be also obtained by simply exchanging $X$ and $Y.$
Define now $\displaystyle\omega=e^{i\frac{2\pi}{5}},$ multiplication by which causes a rotation by $72^{\circ}$ around the origin.
Statement
Assume $\displaystyle\sum_{k=0}^{4}A_{k}=0.$ Define $Q_{i}=(1-\tau )B_{i}+\tau B_{i+1},$ $i \mod 5.$ Then
$Q_{i+1}=wQ_{i},$ $i \mod 5.$
Observe that this exactly says that $Q_0Q_1Q_2Q_3Q_4$ is regular.
Proof
Let's express $\{Q_{i}\}$ explicitly in terms of $\{A_{i}\}.$
$\begin{align}\displaystyle Q_{i}&=(1-\tau )B_{i}+\tau B_{i+1}\\ &=(1-\tau)A_{i}+[(1-\tau )\phi + \tau]A_{i+1}+[(1-\tau )+\tau\phi ]A_{i+2}+\tau A_{i+3}. \end{align}$
It is simpler to collect the coefficients by $A_0,A_1,A_2,A_3,A_4$ (sic!), into a vector such that we may rewrite the above as
$Q_{i}=\bigg((1-\tau),\,(1-\tau )\phi + \tau,\,(1-\tau )+\tau\phi,\,\tau ,\,0\bigg).$
Next
$\omega Q_{i}=\bigg(\omega (1-\tau),\,\omega (1-\tau )\phi + \omega \tau,\,\omega (1-\tau )+\omega \tau\phi,\,\omega \tau ,\,0\bigg).$
Finally, replace $A_{0}$ with $\displaystyle A_{0}=-\sum_{k=1}^{4}A_{k}:$
$\begin{align}\omega Q_{i}=\bigg(0,&\,-\omega (1-\tau)+\omega (1-\tau )\phi + \omega \tau,\\ &-\omega (1-\tau)+\omega (1-\tau )+\omega \tau\phi,\,-\omega (1-\tau)+\omega \tau ,\,-\omega (1-\tau)\bigg). \end{align}$
We may simplify that a little:
$\omega Q_{i}=\bigg(0,\,\omega (2\tau -1)+\omega (1-\tau )\phi,\omega\tau\phi,\,\omega (2\tau -1),\,\omega (\tau -1)\bigg).$
To remind
$Q_{i+1}=\bigg(0,\,(1-\tau),\,(1-\tau )\phi + \tau,\,(1-\tau )+\tau\phi,\,\tau\bigg).$
In order to prove that $\omega Q_{i}=Q_{i+1}$ we need to establish four identities:
$\begin{cases} I: & 1-\tau = \omega (2\tau -1)+\omega (1-\tau )\phi,\\ II: & (1-\tau )\phi + \tau = \omega\tau\phi,\\ III: & (1-\tau )+\tau\phi = \omega (2\tau -1),\\ IV: & \tau = \omega (\tau -1). \end{cases}$
The four identities are not independent. E.g., substituting $\omega (2\tau -1)=(1-\tau )+\tau\phi$ from (III) into (I) we obtain (IV) times $\phi.$ Also, if we multiply (III) by $\phi,$ use $\phi^{2}=1+\phi$ and substitute into that $(1-\tau )\phi=\omega\tau\phi-\tau$ from (II) we again obtain (IV) times $\phi.$ So, at best, only two of these equations are independent - say, (II) and (IV).
Now $\omega (II)+\phi (IV)$ leads to $\omega-\phi=\omega^{2}\phi.$
Several trigonometric identities will serve well to help finish the proof:
$ \displaystyle\omega = \frac{\sqrt{5}-1}{4}+i\sqrt{\frac{5+\sqrt{5}}{8}},\\ \displaystyle\omega^{2}= -\frac{\sqrt{5}+1}{4}+i\sqrt{\frac{5-\sqrt{5}}{8}},\\ \displaystyle\sin 54^{\circ}=\frac{\sqrt{5}+1}{4},\\ \displaystyle\cos 54^{\circ}=\sqrt{\frac{5-\sqrt{5}}{8}}. $
All that needs to be verified now is:
$\omega-\phi=\omega^{2}\phi$ and
$\tau = \omega (\tau -1),$
where $\displaystyle\phi=\frac{\sqrt{5}+1}{2}$ and $\displaystyle \tau=\frac{1}{2}(1+ i\cdot \tan 54^{\circ}).$ Let's check the second one:
$\displaystyle\begin{align} \frac{\tau}{\tau -1} &= \frac{\cos 54^{\circ} +i\sin 54^{\circ}}{-\cos 54^{\circ}+i\sin 54^{\circ}}\\ &=\frac{(\cos 54^{\circ} +i\sin 54^{\circ})^{2}}{1}\\ &=(\sin^{2} 54^{\circ}-\cos^{2}54^{\circ})+2i\cos 54^{\circ}\sin 54^{\circ}\\ &=-\cos 108^{\circ}+i\sin 108^{\circ}\\ &=\cos 72^{\circ}+i\sin 72^{\circ}\\ &=\omega. \end{align}$
Verifying the other identity is left as an exercise.
Acknowledgment
The above construction of the regular pentagon is by Dao Thanh Oai (Vietnam) who posted it at the CutTheKnotMath facebook page.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73573892
