An Inequality in a Convex Quadrilateral
Problem
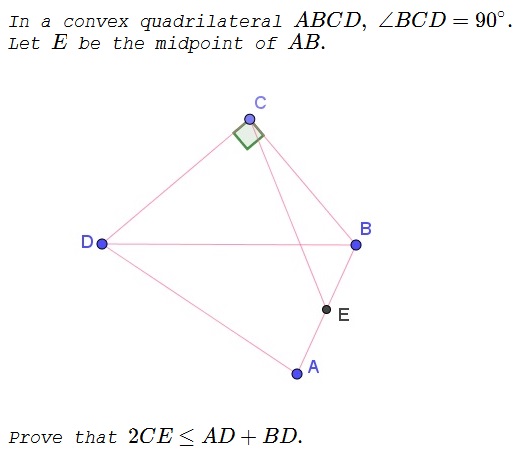
Solution 1
Let $O$ be the midpoint of $BD:$
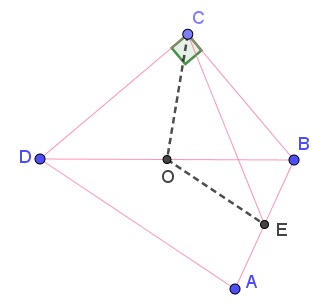
In $\Delta ABD,$ $EO$ is a midline so that $2\cdot EO=AD.$
In $\Delta BCD,$ $2\cdot CO=BD.$
In $\Delta CEO,$ $CE\lt CO+EO.$
Thus a substitution yields the required inequality.
Note that the proof stands if $\angle BCD\gt 90^{\circ}$ because then we have an inequality $2\cdot CO\lt BD$ which is obvious.
Solution 2
Let $C=(0,0),$ $B=(0,1),$ $D=(a,0),$ and $A=(b,c),$ with $a\gt 0$ and $b,c$ arbitrary real. We have
$\displaystyle \begin{align} 2\cdot EC&=\sqrt{b^2+(c+1)^2},\\ 2\cdot AD&=\sqrt{(b-a)^2+c^2},\\ BD&=\sqrt{a^2+1}. \end{align}$
Additionally,
$\sqrt{b^2+(c+1)^2}\le \sqrt{(b-a)^2+c^2}+\sqrt{a^2+1}$
which is equivalent to
$(b-a)a+c\le\sqrt{(b-a)^2+c^2}\cdot\sqrt{a^2+1}.$
The latter is true by the Cauchy-Schwarz inequality.
Solution 3
Let $B'$ be the reflection of $B$ in $C.$
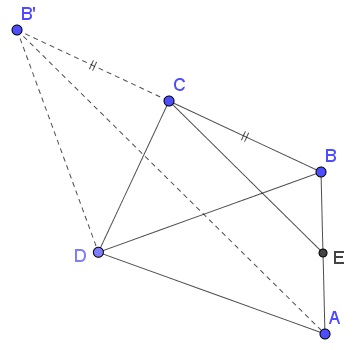
In $\Delta ABB',$ $2\cdot CE=AB$ while, in the isosceles $\Delta BDB',$ $BD=B'D.$ Lastly, in $\Delta AB'D,$
$AD+B'D=AD+BD\gt AB'=2\cdot CE.$
Acknowledgment
This problem from the III Caucasus Mathematic Olympiad (March 15–20, 2018) for Juniors was kindly communicated to me by Leo Giugiuc, along with a solution by Marian Dinca (Solution 1). Leo later added a solution of his (Solution 2).
The problem was devised by D. A. Belov who gave two solutions (Solutions 1 and 3 above).
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73598110
