Yet Another Concurrence on the 9-Point Circle
What Might This Be About?
Problem
Lines $m_a,$ $m_b,$ $m_c,$ are perpendicular to the three parallel lines $l_a,$ $l_b,$ $l_c$. Denote the intersections $P_{ab}=l_{a}\cap m_{b},$ $P_{ba}=l_{b}\cap m_{a},$ $P_{ac}=l_{a}\cap m_{c},$ $P_{ca}=l_{c}\cap m_{a},$ $P_{bc}=l_{b}\cap m_{c},$ $P_{cb}=l_{c}\cap m_{b},$ $A=l_{a}\cap m_{a},$ $B=l_{b}\cap m_{b},$ $C=l_{c}\cap m_{c}.$
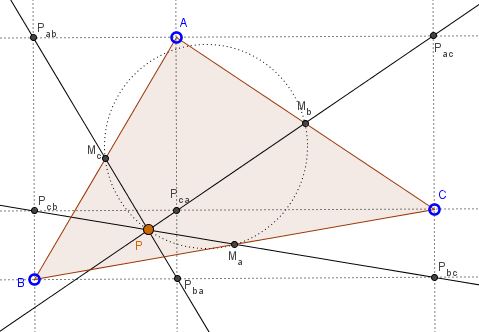
Prove that
Lines $P_{ab}P_{ba},$ $P_{ac}P_{ca},$ $P_{cb}P_{bc}$ are concurrent;
The point of concurrency lies on the 9-point circle of $\Delta ABC.$
Hint
The problem may be solved with relative ease by choosing a convenient coordinate system.
Solution
Assume the given lines are parallel to the coordinate axes, so that the lines are given by the equations:
$l_a:\space y=2n,$ $l_b:\space y=2q,$ $l_c:\space y=2v,$
$m_a:\space y=2m,$ $m_b:\space y=2p,$ $m_c:\space y=2u.$
These determine the coordinates of nine points: $P_{ab}(2p,2n),$ $P_{ba}(2m,2q),$ $P_{bc}(2u,2q),$ $P_{cb}(2p,2v),$ $P_{ca}(2m,2v),$ $P_{ac}(2u,2n),$ $A(2m,2n),$ $B(2p,2q),$ $C(2u,2v).$

The equations of the lines through two given points are found to be
$\begin{align} P_{ab}P_{ba} &:\space x(q-n)+y(p-m)=2(pq-mn),\\ P_{bc}P_{cb} &:\space x(v-q)+y(u-p)=2(uv-pq),\\ P_{ca}P_{ac} &:\space x(n-v)+y(m-u)=2(mn-uv). \end{align} $
The condition for the concurrency of the three lines,
$\left|\begin{array}{ccc} q-n & p-m & pq-mn \\ b-q & u-p & uv-pq \\ n-v & m-u & mn-uv \end{array}\right|=0,$
is easily verified, as, say, the rows of the determinant are clearly linearly dependent (the sum of all three is identically zero.)
The three lines $P_{ab}P_{ba},$ $P_{bc}P_{cb},$ and $P_{ca}P_{ac}$ cross the sides of $\Delta ABC$ at the midpoints, so that $P_{ab}P_{ba}\cap AB=M_c,$ $P_{bc}P_{cb}\cap BC=M_a,$ and $P_{ca}P_{ac}\cap AC=M_b.$ The three midpoints lie on the 9-point circle of $\Delta ABC.$ This allows finding their coordinates, e.g., $M_a(p+u,q+v),$ etc.
In order to prove that the point of concurrency $P$ lies on the 9-point circle suffice it to prove that the four points $P,$ $M_a,$ $M_b,$ $M_c$ are concyclic. One way to do that is to consider the points as complex numbers and establish that the harmonic ratio,
$\displaystyle\frac{M_{a}-P}{M_{b}-P}:\frac{M_{a}-M_{c}}{M_{b}-M_{c}}$
of the four points is real. This is not a difficult exercise in the algebra of complex numbers, as the explicit formula for the harmonic ratio permits significant simplifications.
Acknowledgment
The problem has been pointed to at the CutTheKnotMath facebook page by Antreas Hatzipolakis (Greece); the proof has been supplied by Leonard Giugiuc (Romania).
References
- I. Panakis: 2500 Problems of Geometric Loci With Their Solutions [in Greek]. Athens, ca 1965, p. 654, #582.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73573537
