Concurrence on a Circle

What Might This Be About?

Problem

Let $C(O)$ be a circle in the plane. Let $C(O_1)$ and $C(O_2)$ be two non-intersecting circles touching $C(O)$ internally at points $A$ and $B,$ respectively.

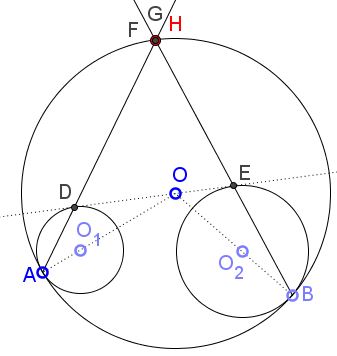
Concurrence on a Circle - problem

Let $t$ be a common tangent of $C(O_1)$ and $C(O_2),$ touching them at points $D$ and $E,$ respectively, such that both $C(O_1)$ and $C(O_2)$ are on the same side of $t.$ Let $F$ be the point of intersection of $AD$ and $BE.$

Show that $F$ lies on $C(O).$

(In fact, the circles $C(O_1)$ and $C(O_2)$ may well cross, without despoiling the problem.)

Solution

Let $G$ be the intersection of $AD$ with $C(O),$ $H$ the intersection of $C(O)$ with $CE.$ We need to show that the three points coincide. To this end, proving $G=H$ will suffice.

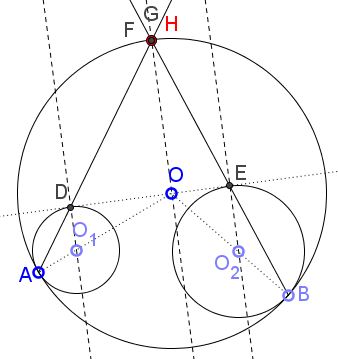
Concurrence on a Circle - solution

Triangles $AO_1D$ and $AOG$ are isosceles,scalene,equal,isosceles with a common base angle at $A.$ They are thus similar,similar,right,equal and have equal apex angles. This makes lines $O_1D$ and $OG$ parallel.

Similarly, $O_2E\parallel OH.$

But, since $O_1D\perp t\perp O_2E,$ this is also true that $O_1D$ is parallel,perpendicular,parallel,tangent $O_2E,$ making $OG\parallel OH$ which is only possible if $G=H,$ as required.

Acknowledgment

This is one of the problems from the book Jim Totten's Problems of the Week in memory of Jim Totten, a long time Problem Editor and later Editor-in-Chief of Crux Mathematicorum.

References

J. G. McLoughlin et al, Jim Totten's Problems of the Week, World Scientific, 2013, #309

71548467