Circle Rotations and Fixed Points
What is this about?
Problem
A given a circular arc $BS$ is rotated through a given angle into position $BS'.$
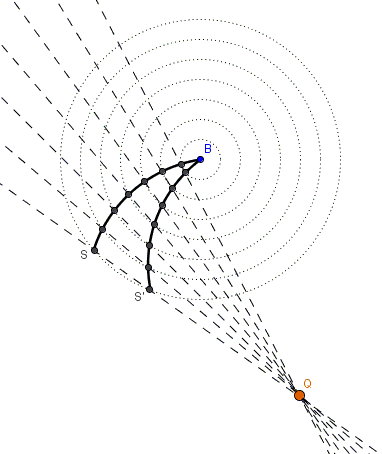
Prove that the straight lines through the pairs of points corresponding under the rotation all pass through a fixed point.
Hint
Extend the arcs to complete circles and prepare to "chase" inscribed angles.
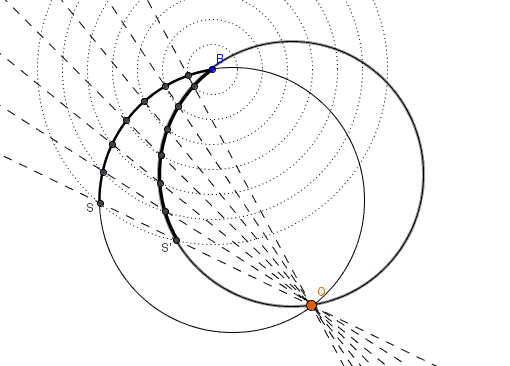
Solution
Consider two circles with centers $A$ and $A'$ that cross at points $B$ and $Q.$
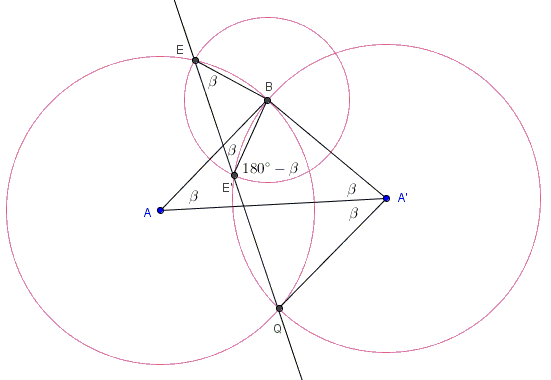
The two circles can be seen as obtained by a rotation around point $B.$ Let $E$ and $E'$ be a pair of points corresponding under the rotation such that $\angle EBE'=\angle ABA'.$ This makes isosceles triangles $EBE'$ and $ABA'$ similar. Let $\beta$ be their base angle. In particular, $BE'E=\beta$ and also $BA'A=\beta.$ Their is a symmetry in the line $AA'$ that joins the centers of the circles, implying $\angle AA'Q=\beta.$
In circle $(A')$, arc $BE'Q=2\beta,$ leaving the complement of $360^{\circ}-2\beta$ and implying that for the inscribed angle $BE'Q=180^{\circ}-\beta.$ This means that angles $BE'E$ and $BE'Q$ are supplementary and points $E,E',Q$ are collinear. In other words, line $EE'$ passes through $Q.$
Acknowledgment
The problem was inspired by a post by Emmanuel Antonio José García at the CutTheKnotMath facebook page.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581454
