Concyclic Points from Midpoint of an Arc
What is this about?
Problem
In circle $A(B)$, centered at $A$ and passing through $B$, $B$ is the midpoint of arc $CC'.$ $D$ and $E$ are points on the circle. $BD$ cuts $CC'$ in $F,$ $BE$ in $G.$
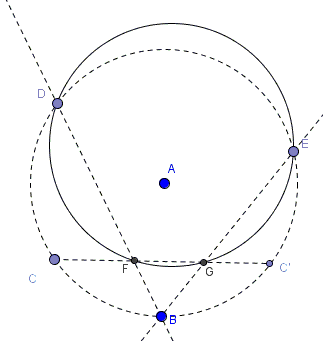
Prove points $D,$ $E,$ $F,$ $G$ concyclic.
Hint
Think of inscribed, secant angles and angle chasing.
Solution
To prove the required concyclicity suffice it to show that $\angle DFG+\angle DEG=180^{\circ}.$
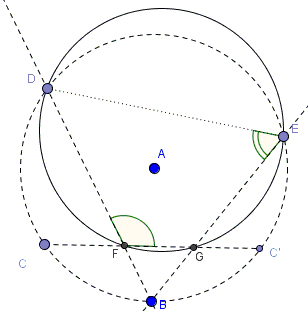
In terms of arcs,
$ \begin{align} \angle DFG &= \angle DFC' \\ &=({DEC'}+{BC})/2 \\ \end{align} $
While,
$ \begin{align} \angle DEG &= \angle DEB \\ &=({CD}+{BC})/2 \\ &=({CD}+{C'B})/2 \\ \end{align} $
The arcs involved cover the whole circle and, hence, add up to $360^{\circ}.$
Acknowledgment
The problem is from the Geometry in Pictures by A. V. Akopyan. The book is in Russian but this should not scare anyone, for it is a collection of suggestive geometric diagrams with no description, let alone description in Russian.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581622
