Characterization of Trapezoid

What Might This Be About?

Problem

The midline $EF$ of a convex quadrilateral $ABCD$ divides its area into equal parts.

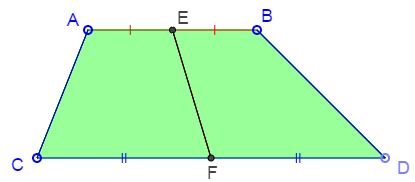
area of a quadrilateral is halved by the midline, problem

Prove that $ABCD$ is a trapezoid.

Proof

Let $[X]$ denote the area of figure $X.$

Since $AE=BE,$ $[\Delta AEF]=[\Delta BEF].$ Since it is given that $[ACFE]=[BDFE],$ taking the difference we see that $[\Delta ACF]=[\Delta BDF].$

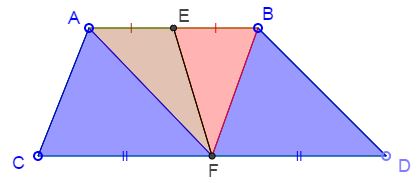
area of a quadrilateral is halved by the midline, solution

But the two triangles have equal bases $CF=DF,$ implying that their altitudes to the bases are also equal, i.e., $A$ and $B$ are at the sam distance from $CD.$ Hence $AB\parallel CD.$

References

V.V. Proizvolov, Zadachi na vyrost (Russian. Problems to grow up with), Miros, Moscow, 1995, ISBN 5708401133, p 7

72340187