Cevians Through the Circumcenter
Problem
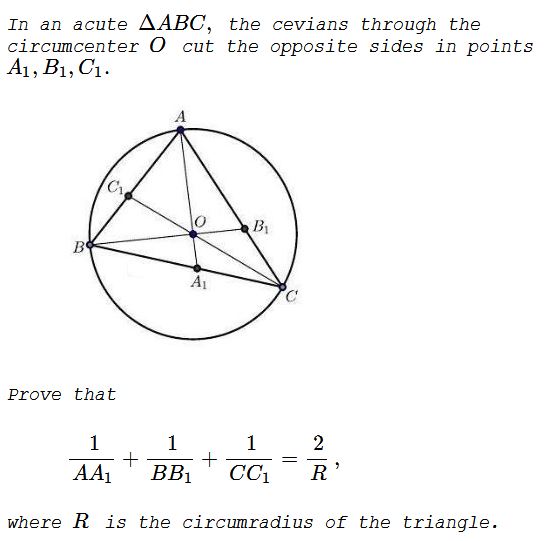
Proof 1
$\displaystyle\frac{R}{OA_1}=\frac{AO}{OA_1}=\frac{AC_1}{C_1B}+\frac{AB_1}{B_1C}.\,$ But $\displaystyle\frac{AC_1}{C_1B}=\frac{[AOC]}{[BOC]}=\frac{\sin 2B}{\sin 2A}\,$ and, similarly, $\displaystyle\frac{AB_1}{B_1C}=\frac{\sin 2C}{\sin 2A},\,$ implying $\displaystyle\frac{R}{OA_1}=\frac{\sin 2B+\sin 2C}{\sin 2A},\,$ i.e., $\displaystyle\frac{R}{AA_1}=\frac{\sin 2B+\sin 2C}{\sin 2A+\sin 2B+\sin 2C}\,$ and, finally,
$\displaystyle\frac{1}{AA_1}=\frac{1}{R}\frac{\sin 2B+\sin 2C}{\sin 2A+\sin 2B+\sin 2C}.$
Similarly,
$\displaystyle\frac{1}{BB_1}=\frac{1}{R}\frac{\sin 2A+\sin 2C}{\sin 2A+\sin 2B+\sin 2C},\\ \displaystyle\frac{1}{CC_1}=\frac{1}{R}\frac{\sin 2A+\sin 2B}{\sin 2A+\sin 2B+\sin 2C}.$
Adding all three yields the required result.
(The above reminds of a second proof of another interesting fact, concerning cocurrent cevians.)
Proof 2
We_1ll be using the following
Lemma
In the diagram below, $\displaystyle\frac{XP}{XQ}=\frac{[YXZP]}{[XYZ]}.$
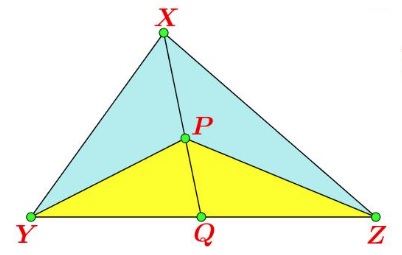
By the lemma,
$\displaystyle\begin{align} \frac{R}{AA_1}+\frac{R}{BB_1}+\frac{R}{CC_1} &= \frac{AO}{AA_1}+\frac{BO}{BB_1}+\frac{CO}{CC_1}\\ &=\frac{[BACO]}{[ABC]}+\frac{[CBAO]}{[ABC]}+\frac{[ACBO]}{[ABC]}\\ &=\frac{2[ABC]}{[ABC]}\\ &=2. \end{align}$
And the result follows.
Proof 3
We have $OD=OA_1\cos\omega\,$ and $\cos\angle BOD=\cos A=\displaystyle\frac{OD}{R}.\,$ So
(*)
$OA'\cos\omega=R\cos A.$
Also, $\angle BOD +\omega=2\varphi=\pi-\angle AOB=\pi-2C\,$ (see the figure) so that $A+\omega=\pi-2C,\,$ which is $\omega=B-C.$
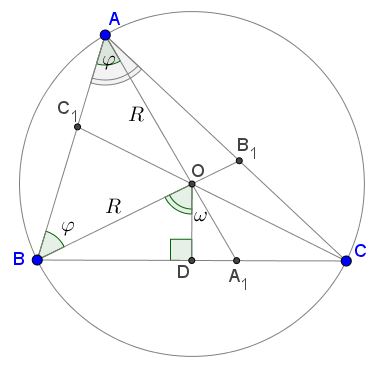
Now from (*) we have $OA_1=\displaystyle\frac{R\cos A}{\cos (B-C)}.\,$ So that
$AA_1=R+OA_1=R\displaystyle\frac{\cos A+\cos (B-C)}{\cos (B-C)}=\frac{2R\sin B\sin C}{\cos B\cos C+\sin B\sin C},$
which is $\displaystyle\frac{1}{AA_1}=\frac{1}{2R}(\cot B\cot C+1).\,$ Similarly,
$\displaystyle\frac{1}{BB_1}=\frac{1}{2R}(\cot C\cot A+1), \displaystyle\frac{1}{CC_1}=\frac{1}{2R}(\cot A\cot B+1).$
Adding up the three identities we get
$\displaystyle\frac{1}{AA_1}+\frac{1}{BB_1}+\frac{1}{CC_1}=\frac{1}{2R}\left(3+\sum_{cycl}\cot A\cot B\right).$
It is well know that $\displaystyle\sum_{cycl}\cot A\cot B=1\,$ which delivers the required
$\displaystyle\frac{1}{AA_1}+\frac{1}{BB_1}+\frac{1}{CC_1}=\frac{2}{R}.$
Extension into 3D
In a tetrahedron $ABCD,\,$ inscribed into a sphere $(O),\,$ so that $O\,$ is strictly inside the tetrahedron, the cevians through the circumcenter $O\,$ cut the opposite sides in points $A_1, B_1,C_1, D_1.\,$
Prove that
$\displaystyle\frac{1}{AA_1}+\frac{1}{BB_1}+\frac{1}{CC_1}+\frac{1}{DD_1}=\frac{3}{R},$
where $R\,$ is the radius of the sphere.
Let $[OBCD]=x,\,$ $[OACD]=y,\,$ $[OABD]=z,\,$ and $[OABC]=t.\;$ Then
$\displaystyle\frac{R}{OA_1}=\frac{A}{OA_1}=\frac{y+z+t}{x},$
implying $\displaystyle\frac{R}{AA_1}=\frac{y+z+t}{x+y+z+t},\,$ i.e., $\displaystyle\frac{1}{AA_1}=\frac{1}{R}\left(\frac{y+z+t}{x+y+z+t}\right).\,$ Simialrly,
$\displaystyle \frac{1}{BB_1}=\frac{1}{R}\left(\frac{x+z+t}{x+y+z+t}\right),\\ \displaystyle \frac{1}{CC_1}=\frac{1}{R}\left(\frac{x+y+t}{x+y+z+t}\right),\\ \displaystyle \frac{1}{DD_1}=\frac{1}{R}\left(\frac{x+y+z}{x+y+z+t}\right).$
Now add all four to obtain the desired result.
Remark
A more general result is well known:
For three cevians concurrent at point $P,$
$\displaystyle\frac{AP}{AA_1}+\frac{BP}{BB_1}+\frac{CP}{CC_1}=2,\\ \displaystyle\frac{A_1P}{AA_1}+\frac{B_1P}{BB_1}+\frac{C_1P}{CC_1}=1.$
A proof can be easily obtained form Migual Ochoa Sanchez's Lemma. In 3D, as Leo Giugiuc proof shows, a generalization is also available:
In a tetrahedron $ABCD,\,$ inscribed into a sphere $(O),\,$ so that $O\,$ is strictly inside the tetrahedron, the cevians through the circumcenter $O\,$ cut the opposite sides in points $A_1, B_1,C_1, D_1.\,$
Prove that
$\displaystyle\frac{AP}{AA_1}+\frac{BP}{BB_1}+\frac{CP}{CC_1}+\frac{DP}{DD_1}=3.$
Acknowledgment
This problem by Nguyen Viet Hung (Vietnam) has kindly posted at the CutTheKnotMath facebook page by Leo Giugiuc (Romania), along with a solution (Proof 1) and later commented on by Miguel Ochoa Sanchez (Peru) with Proof 2. Proof 3 is by George Apostolopoulos (Greece) and was communicated via facebook messaging. The extension into 3D was conceived by Marian Dinca (Romania). The solution is by Leo Giugiuc.
I've been notified (after posting at facebook) by Takis Chronopoulos of a discussion at the mathematica.gr forum of a discussion that started on June 23, 2011 with exactly the above question. Among the solutions that were found Proof #3 was featuring prominently.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73518174
