Hidden Orthogonality
What Might This Be About?
Problem
Let $ABCD$ be a cyclic quadrilateral; $E$ the intersection $AB\cap CD,$ $F=BC\cap AD;$ $FG$ and $EH$ tangent to the circumcircle $(ABCD).$
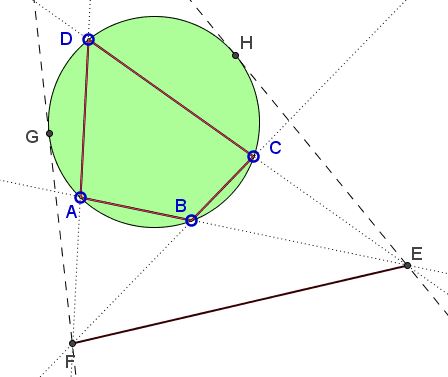
Prove that
$EH^{2}+FG^{2}=EF^{2}.$
Solution
Draw circles $(BCE)$ and $(CDF)$ and let $Q$ be their second point of intersection.
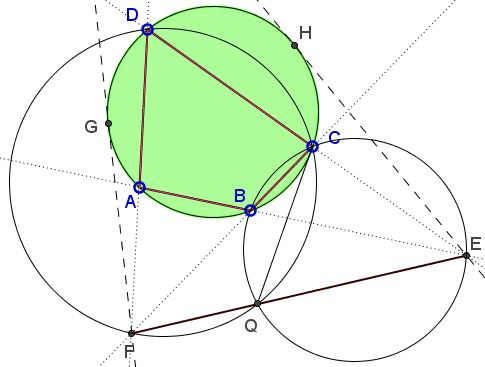
Point $Q$ lies on $EF$. Indeed, $\angle CQE=\angle CBE$ as inscribed into $(BCE)$ and subtended by the same arc. Angles $CQF$ and $ABC$ are both supplementary to $\angle ADC,$ while $\angle ABC$ is also supplementary to $\angle CBE.$ It follows that $\angle CQF + \angle CQE=180^{\circ},$ such that $EQF$ is a straight line.
Next we repeatedly apply the Power of a Point Theorem:
$\begin{array}{lcl} \mbox{in}\space(ABCD) & & FG^{2}=FB\cdot FC,\\ \mbox{in}\space(BCE) & & FB\cdot FC = FQ\cdot FE,\\ \mbox{in}\space(ABCD) & & EH^{2}=EC\cdot ED,\\ \mbox{in}\space(CDF) & & EC\cdot ED=EQ\cdot EF. \end{array}$
It follows that
$FG^{2}+EH^{2}=FQ\cdot FE+EQ\cdot EF=EF\cdot(FQ+EQ)=EF^{2}.$
A natural interpretation of this result is that circles $C(E,H),$ centered at $E$ through $H$, and $C(F,G),$ centered at $F$ through $G,$ are orthogonal.
Acknowledgment
The problem has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page with a reference to a video by Francisco Javier García Capitán. The solution is by Joseph García Piscoya
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73573207
