Problem CC156 From Crux Mathematicorum
Problem
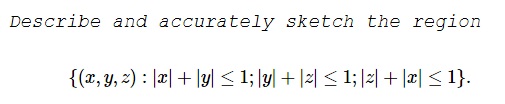
Solution
If the feasible region is constructed in the first octant, the feasible region can be extended to the other octants using symmetry (flipping the signs of $x$, $y$, and $z$, one at a time).
Consider the sides of the planes $x+y=1$, $y+z=1$, and $z+x=1$ that contain the origin. The intersection of the three regions is the feasible region in the first octant.
Any two of these three planes intersect in a line. For example, the planes $x+y=1$ and $y+z=1$ intersect in the line with $x=z$ and $y=1-z$. The remaining two combinations can be written down by cyclically permuting the variables.
The only point where all the three planes and thus the three lines meet is $(1/2,1/2,1/2)$.
In the figure, O:$(0,0,0)$, A:$(1,0,0)$, B:$(0,1,0)$, C:$(0,0,1)$, P:$(1/2,1/2,1/2).$ $PAB,$ $PBC,$ $PCA$ are the planes $x+y=1,$ $y+z=1,$ $z+x=1,$ respectively. The common point is $P$. The line segments associated with the plane intersections are also visible.
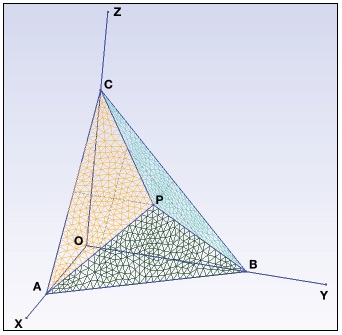
Using symmetry, we get the feasible region (the outer boundary is shown in the figure below).

Illustration
Acknowledgment
This is problem CC156 (Contest Corner 156) from the Canadian Crux Mathematicorum. The solution is by Amit Itagi, the illustration by N. N. Taleb. A follower Eddie on twitter identified the shape as rhombic dodecahedron.
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73583699
