Areas in Two Parallelograms and a Translation
What is this about?
Problem
$ABCD$ and $GHIJ$ are two parallelograms. $G'H'I'J'$ is a translation of $GHIJ$ and lies entirely within $ABCD.$ Let $[X]$ denote the area of figure $X.$
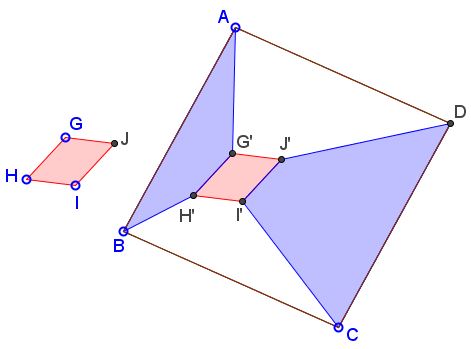
Then $[ABH'G']+[CDJ'I']$ does not depend on the position of $G'H'I'J'$ within $ABCD.$
Proof
Split the quadrilaterals $ABH'G'$ and $CDJ'I'$ into two triangles as shown.
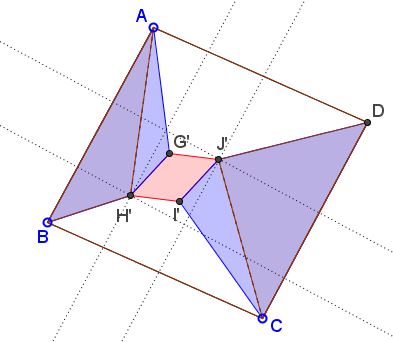
The required result follows from a more basic assertion, namely, that $[\Delta ABH']+[\Delta CDJ']$ does not depend on the position of $G'H'I'J'$ within $ABCD$ and the same holds for $[\Delta AG'H']+[\Delta CI'J'].$ I'll prove the former one first.
Let $h,g$ be the distances from $H'$ to $AB$ and from $J'$ to $CD,$ respectfully. Let $k$ be the distance between two lines (one through $H',$ the other through $J')$ parallel to $AB.$ Then $h+g+k$ equals the distance between $AB$ to $CD.$ And, since $k$ is constant, so is $h+g.$ Now,
$[\Delta ABH']+[\Delta CDJ']=\frac{1}{2}(AB\cdot h+CD\cdot g)=\frac{1}{2}AB(h+g)$
which is constant. Now for the second identity $[\Delta AG'H']+[\Delta CI'J'].$
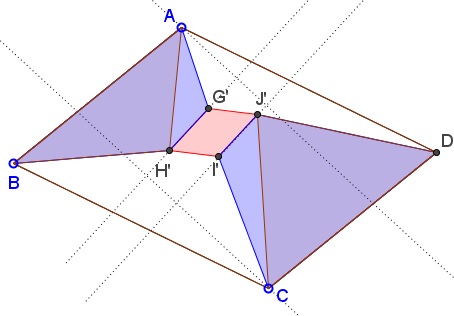
The argument is similar to the foregoing one. Let $r,s,t$ be the lengths of the perpendiculars from $A$ to $G'H',$ from $C$ to $I'J',$ and $t$ the distance between $G'H'$ and $I'J'.$ For fixed directions, $r+s+t$ is constant and so is $r+s.$ On the other hand,
$[\Delta AG'H']+[\Delta CI'J']=\frac{1}{2}(G'H'\cdot r+I'J'\cdot s)=\frac{1}{2}GH(r+s),$
which is constant.
Remark
When both $ABCD$ and $GHIJ$ are squares the above leads to additional results.
Assume both $ABCD$ and $GHIJ$ are squares:
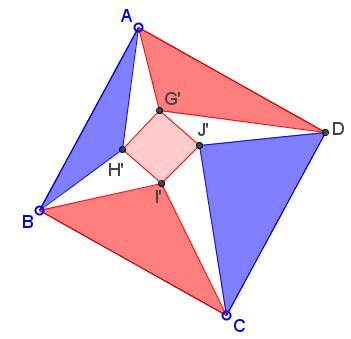
Then:
$[\Delta ADG']+[\Delta CBI']=[\Delta ABH']+[\Delta CDJ'],$
$[\Delta AG'H']+[\Delta CI'J']=[\Delta BH'I']+[\Delta DG'J'].$
Extension
The above remains true if the two shapes remain invariant under a rotation by $90^{\circ}.$ For example, Tran Quang Hung has generalized the foregoing claims as illustrated below
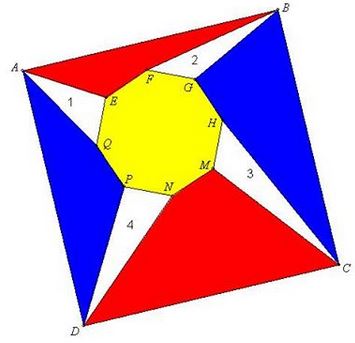
and
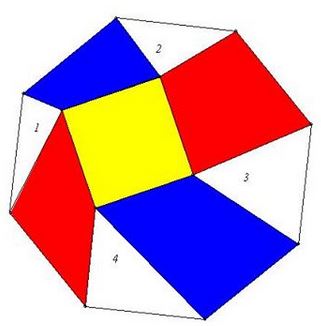
Tran Quang Hung has extended the statements to the case of two even sided polygons.
Acknowledgment
The problem has been posted by Tran Quang Hung at the CutTheKnotMath facebook page.
![]()
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny73581832
