Areas in Three Squares
Source

Problem
Given three squares $AMNP,$ $ABCD,$ and $DPQR.$
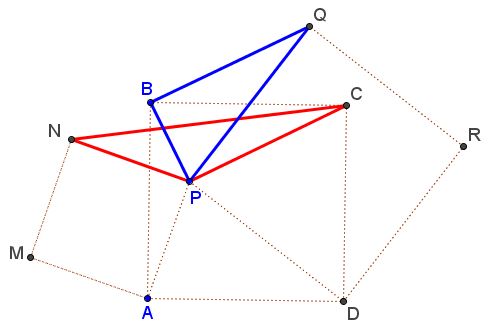
Prove that $[\Delta CPN]=[\Delta BPQ],$ where $[X]$ denotes the area of shape $X.$
Solution 1
The solution is illustrated by a sequence of diagrams.
Draw $BF\parallel PQ$ and $CG\parallel NP$ $(F$ on $QR$ or its extension; $G$ on $MN$ or its extension. Then $[\Delta CPN]=[\Delta GPN]$ and $[\Delta BPQ]=[\Delta FPQ]:$
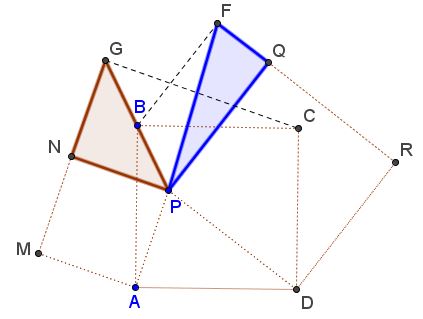
$M,$ $B,$ $F$ are collinear as are $R,$ $C,$ $G.$ This has been shown elsewhere:
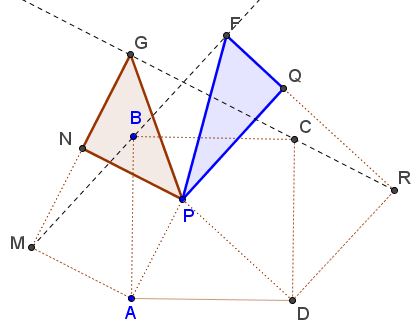
Complete the triangles $GPN$ and $FPQ$ to rectangles $GEPN$ and $FHPQ.$
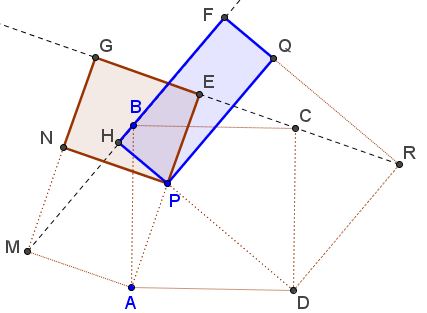
We'd like to show that $[GEPN]=[FHPQ],$ i.e., that $EP\cdot NP = HP\cdot PQ.$ Consider the circles $(MP)$ and $(PR),$ with diameters $MP$ and $PR,$ respectively.
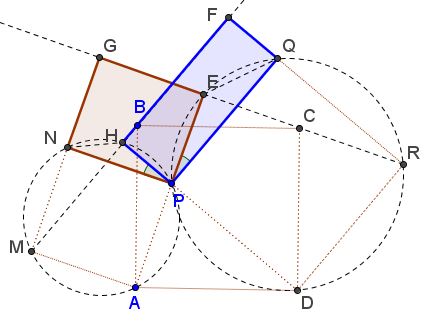
Obviously, $A,N\in (MP)$ but also $H\in (MP).$ Similarly, $D,Q,E\in (PR).$ Observe that
$\angle HPN=\angle HMN=\angle GRF=\angle EPQ.$
In addition, $\angle NHP=\angle PEQ=135^{\circ}$ because both (inscribed) angles are subtended by the sides of squares inscribed into the circles $(MP)$ and $(PR).$ It follows that triangles $HNP$ and $EPQ$ are similar, from which we have the proportion $\displaystyle\frac{HP}{NP}=\frac{EP}{PQ}$ which is equivalent to $EP\cdot NP = HP\cdot PQ.$
Solution 2
We choose $A=-1+-i,$ $B=-1+i,$ $C=1+i,$ $D=1-i,$ and $P=a+bi,$ where $-1\lt a,b\lt 1.$
First of all, $\displaystyle\frac{N-P}{A-P}=-i,$ implying $N=(a-b-1)+i(a+b+1).$ Similarly, $\displaystyle\frac{Q-P}{D-P}=i,$ implying $Q=(a+b+1)+i(-a+b+1).$ Further,
$2[\Delta BPQ]=\left|\begin{array}{ccc} a & b & 1\\ a+b+1 & -a+b+1 & 1\\ -1 & 1 & 1 \end{array}\right|=2-(a^2+b^2).$
Similarly, $2[\Delta PNC]=2-(a^2+b^2).$
Solution 3
Let $[\overrightarrow{u}]$ be the image of an arbitrary vector $\overrightarrow{u}$ under the rotation through $90^{\circ}$ counterclockwise.
Since $[\Delta PCN]=\frac{1}{2}\left|\overrightarrow{PC}\times\overrightarrow{PN}\right|$ and $[\Delta PQB]=\frac{1}{2}\left|\overrightarrow{PQ}\times\overrightarrow{PB}\right|,$ we have to proe that
(*)
$\overrightarrow{PC}\times\overrightarrow{PN}=\overrightarrow{PQ}\times\overrightarrow{PB}.$
Let $\overrightarrow{PA}=\overrightarrow{a}$ and $\overrightarrow{PD}=\overrightarrow{b}.$ Then $\overrightarrow{PQ}=[\overrightarrow{b}],$ $\overrightarrow{PN}=-[\overrightarrow{a}],$ $\overrightarrow{PB}=\overrightarrow{a}+[\overrightarrow{b}]-[\overrightarrow{a}],$ and $\overrightarrow{PC}=\overrightarrow{b}+[\overrightarrow{b}]-[\overrightarrow{a}].$ We thus have
$\overrightarrow{PC}\times\overrightarrow{PN}=-\overrightarrow{b}\times [\overrightarrow{a}]-[\overrightarrow{b}]\times [\overrightarrow{a}],\\ \overrightarrow{PQ}\times\overrightarrow{PB}=[\overrightarrow{b}]\times \overrightarrow{a}-[\overrightarrow{b}]\times [\overrightarrow{a}].$
So (*) is equivalent to $[\overrightarrow{a}]\times \overrightarrow{b}=[\overrightarrow{b}]\times \overrightarrow{a},$ which is obvious.
Acknowledgment
The problem due to Miguel Ochoa Sanchez has been posted at the CutTheKnotMath facebook page by Leo Giugiuc. The second solution is by Claudia Nanuti, Diana Trailescu, Dan Sitaru and Leo Giugiuc. Solution 3 is by Nevena Sybeva.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581079
