Anticenter and Orthocenters

What Might This Be About?

Problem

Given cyclic quadrilateral $ABCD,$ $H_A$ as the orthocenter of $\triangle BCD,$ and $H_B,$ $H_C,$ $H_D$ are defined cyclically. Let $T$ be the anticenter of $ABCD.$

Anticenter and Orthocenters - problem

Then $T$ is the common midpoint of $AH_A,$ $BH_B,$ $CH_C,$ and $DH_D.$

Solution

We'll show that $AH_A$ and $BH_B$ have the same midpoint. To see that, note that $ABH_AH_B$ is a parallelogram. This is because, on the one hand, $AH_B$ and $BH_A,$ both being perpendicular to $CD$ are parallel.

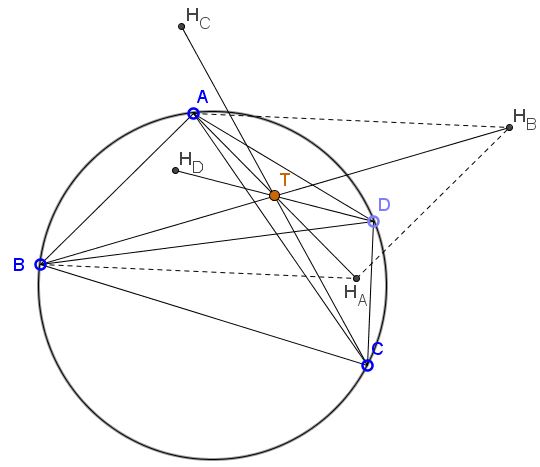
Anticenter and Orthocenters - solution

On the hand, they are equal, since

$AH_B=2R\cdot |\cos\angle CAD|=2R\cdot |\cos\angle CBD|=BH_A,$

where $R$ is the circumradius of the quadrilateral $ABCD.$ Thus, indeed, $ABH_AH_B$ is a parallelogram and its diagonals $AH_A$ and $BH_B$ cross at their common midpoint. Similar argument works for the other pairs of segments $AH_A,$ $BH_B,$ $CH_C,$ and $DH_D.$

Acknowledgment

The theorem and the proof come from the paper Newton and Midpoints of Diagonals of Circumscriptible Quadrilaterals by Titu Andreescu, Luis Gonzales and Cosmin Pohoata (Theorem 2).

72104485