Another Seven Circles Theorem
What Might This Be About?
Problem
Let $A_i,$ $i=1,2,\ldots,6,$ be six points on a circle. Taking subscripts modulo $6,$ we denote, for $i=1,2,\ldots,6,$ the intersections of the lines $A_{i}A_{i+1}$ and $A_{i+2}A_{i+3}$ by $B_{i+3},$ and the circumcenter of the triangles $A_{i}A_{i+1}B_{i+2}$ by $C_{i+3}.$
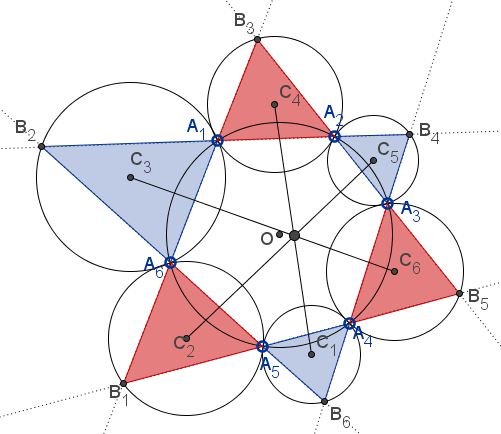
Prove that the lines $C_1C_4,$ $C_2C_5,$ and $C_3C_6$ are concurrent.
Lemma
If $A,B,C,D$ are points on the unit circle with affixes (associated complex numbers) $a,b,c,d,$ respectively, and the lines $AB$ and $CD$ intersect at $E,$ then the circumcenter $P$ of triangle $ACE$ has affix $\displaystyle p=\frac{ac(b-d)}{ab-cd},$
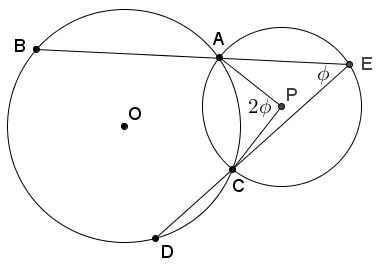
If the oriented angle between $\overrightarrow{AB}$ and $\overrightarrow{CD}$ is $\phi =\angle AEC,$ then $\angle APC=2\phi.$ if $z=\cos\phi +i\sin\phi,$ then since for a point $X$ on the unit circle, the conjugate of its affix $\displaystyle\overline{x}=\frac{1}{x},$ we conclude that
(*)
$(c-p)=(a-p)z^{2}.$
Now, we obtain a sequence of identities:
$\displaystyle\frac{d-c}{|d-c|}=\frac{b-a}{|b-a|}z,\,\frac{(d-c)^{2}}{|d-c|^{2}}=\frac{(b-a)^{2}}{|b-a|^{2}}z^{2},\\$ $\displaystyle\frac{d-c}{\overline{d}-\overline{c}}=\frac{b-a}{\overline{b}-\overline{b}}z,\,\frac{d-c}{\frac{1}{d}-\frac{1}{c}}=\frac{b-a}{\frac{1}{b}-\frac{1}{a}}z^{2},$
and, finally, $cd=abz^{2}.$ From (*), $(c-p)ab=(a-p)cd,$ or, $p(ab-cd)=abc-acd,$ and the lemma follows.
Proof of the statement
To avoid inconvenience of subscripts, we reformulate the statement as follows:
Let $A,B,C,X,Y,Z$ be six points on the unit circle with affixes $a,b,c,x,y,z,$ respectively. The lines $ZB,$ $XC,$ $YA,$ and $CY,$ $AZ,$ $BX$ bound triangles $A'B'C'$ and $A''B''C''.$ If $A_1,$ $B_1,$ $C_1,$ $A_2,$ $B_2,$ $C_2$ are the circumcenters of the circles $(A'YC),$ $(B'ZA),$ $(C'XB),$ $(A''BZ),$ $(B''CX),$ $(C''AY)$
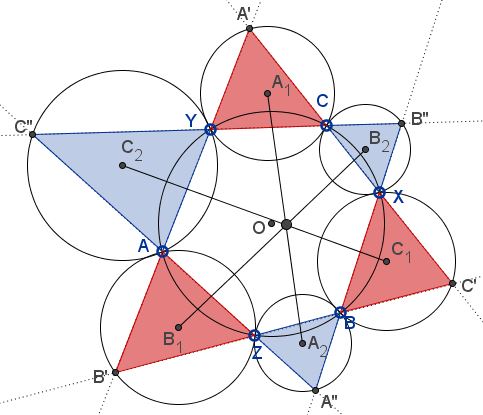
Then the lines $A_{1}A_{2},$ $B_{1}B_{2},$ $C_{1}C_{2}$ are concurrent.
The lemma provides the affixes of the circumcenters:
$\begin{align}\displaystyle a_{1}=\frac{cy(x-a)}{cx-ay}, & \,a_{2}=\frac{bz(a-x)}{az-bx},\\ b_{1}=\frac{az(y-b)}{ay-bz}, & \,b_{2}=\frac{cx(b-y)}{bx-cy},\\ c_{1}=\frac{bx(z-c)}{bz-cx}, & \,c_{2}=\frac{ay(c-z)}{cy-az}. \end{align}$
For every point $W$ on line $A_{1}A_{2}$, the number $\displaystyle t=\frac{w-a_1}{w-a_2}$ is real. Therefore, also $\displaystyle t=\frac{\overline{w}-\overline{a_1}}{\overline{w}-\overline{a_2}}.$ This gives t he equation of the line as
$\begin{vmatrix} w & \overline{w} & 1\\ a_1 & \overline{a_1} & 1\\ a_2 & \overline{a_2} & 1 \end{vmatrix}=0.$
Since $a,b,c,x,y,z$ are on the unit circle,
$\displaystyle\overline{a_{1}}=\frac{\overline{c}\overline{y}(\overline{x}-\overline{a})}{\overline{c}\overline{x}-\overline{a}\overline{y}}=\frac{\frac{1}{c}\frac{1}{y}(\frac{1}{x}-\frac{1}{a})}{\frac{1}{c}\frac{1}{x}-\frac{1}{a}\frac{1}{y}}=\frac{x-a}{cx-ay}.$
Similarly $\displaystyle\overline{a_{2}}=\frac{a-x}{az-bx}.$ From these we obtain the equation of lne $A_{1}A_{2},$ and likewise those of $B_{1}B_{2}$ and $C_{1}C_{2}.$ These are
$(az+cx-ay-bx)w+(bcxy+abyz-cayz-bczx)\overline{w}+(a-x)(cy-bz)=0,\\ (bx+ay-bz-cy)w+(cayz+bczx-abzx-caxy)\overline{w}+(b-y)(az-cx)=0,\\ (cy+bz-cx-az)w+(abzx+caxy-bcxy-abyz)\overline{w}+(c-z)(bx-ay)=0.$
The three lines are concurrent if and only if the determinant of the coefficients vanishes:
$\begin{vmatrix} az+cx-ay-bx & bcxy+abyz-cayz-bczx & (a-x)(cy-bz)\\ bx+ay-bz-cy & cayz+bczx-abzx-caxy & (b-y)(az-cx)\\ cy+bz-cx-az & abzx+caxy-bcxy-abyz & (c-z)(bx-ay) \end{vmatrix}=0.$
This is clearly the case since each column sum equals $0.$
As a side note, from the equations of the lines it is clear that the point of concurrency lies at the origin if and only if
$(a-x)(cy-bz)=(b-y)(az-cx)=(c-z)(bx-ay)=0.$
Assuming points $A,B,C,X,Y,Z$ distinct, this condition is satisfied precisely when their affixes satisfy
$\displaystyle\frac{x}{a}=\frac{y}{b}=\frac{z}{c},$
meaning that $XYZ$ is obtained from $ABC$ by rotation.
Acknowledgment
The problem has been posted by Dao Thanh Oai at the CutTheKnotMath facebook page. The solution is by Nikolaos Dergiades (Dao’s Theorem on Six Circumcenters associated with a Cyclic Hexagon, Forum Geometricorum, Volume 14 (2014) 243–246.) I am grateful to Dao Thanh Oai and Emmanuel Antonio José García for bringing this article up at the CutTheKnotMath facebook page.
Telv Cohl has later published A Purely Synthetic Proof of Dao’s Theorem on Six Circumcenters Associated with a Cyclic Hexagon.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73580780
