Problem 4096 from Crux Mathematicorum
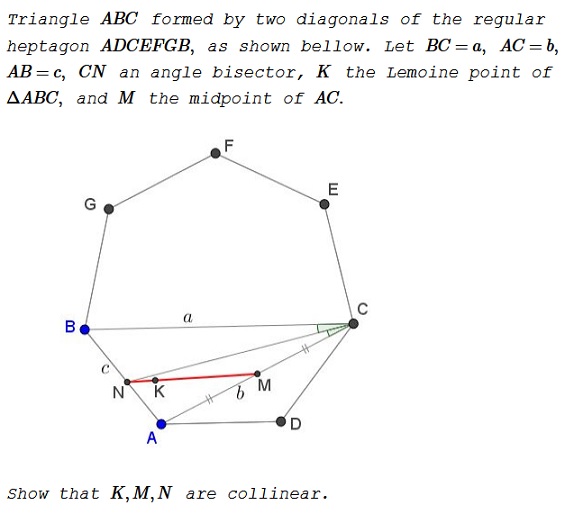
Problem
Solution
In barycentric coordinates, relative to $\Delta ABC,\,$ $N=(a:b:0),\,$ $K=(a^2:b^2:c^2),\,$ $M=(1:0:1).\,$ For the three points to be collinear it is necessary and sufficient to have
$\left|\begin{array}{ccc}a&a^2&1\\b&b^2&0\\0&c^2&1\end{array}\right|=0,$
which is equivalent to
(1)
$c^2+ab=a^2.$
Consider the cyclic quadrilateral $ABEC.\,$
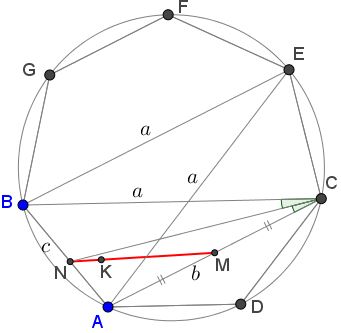
Since, $ADCEFB\,$ is a regular heptagon, $CE=AB=c\,$ and $EB=EA=BC=a.\,$ Applying Ptolemy's theorem to quadrilateral $ABEC\,$ we have
$AB\cdot CE+AC\cdot BE=BC\cdot EA.$
which is $c\cdot c+b\cdot a=a\cdot a,\,$ i.e., (1). Thus the three points are indeed collinear.
Acknowledgment
This is Problem 4096 from Crux Mathematicorum, V. 42, NO. 10 December 2016. The problem is by Kadir Altintas. The solution is by Michel Bataille and Titu Zvonaru.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73580424
