Abutting Equilateral Triangles on a Line I
What is this about?
Problem
Points $A,C,B\space$ are collinear; triangles $ACB_1,$ $ACB_2,$ $CBA_1,$ $CBA_2$ are equilateral.
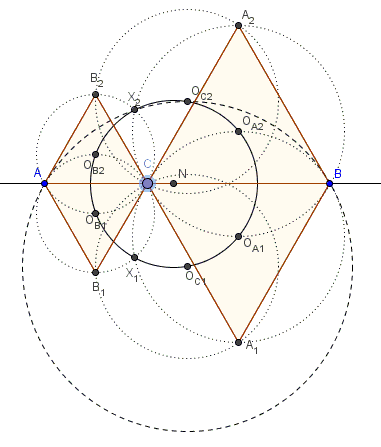
The circumcenters $O_{B1},O_{B2},O_{A1},O_{A2},O_{C1},O_{C2}$ of triangles $ACB_1,$ $ACB_2,$ $CBA_1,$ $CBA_2,$ $A_1B_1C,$ $A_2B_2C$ are concyclic on a circle $(N)$. The intersections $X_1$ of $ACB_1$ and $CBA_1$ and $X_2$ the intersection of $ACB_2$ and $CBA_2$ also lie on $(N).$
In addition, $X_1$ lies on $(ABO_{C1})$ and $X_2$ on $(ABO_{C2}).$
Hint
The circumcenters of triangles $A_1B_1C,$ $A_2B_2C$ do not depend on the position of $C$ on $AB.$ Why?
Also, the configuration of the three points $A,C,B$ amounts to a degenerate triangle to which one may apply Napoleon's theorem.
Solution
Points $A,C,B$ form two degenerate triangles. $O_{B2},$ $O_{A2},$ and $O_{C1}$ are the centers of Napoleon's triangles for one while $O_{B1},$ $O_{A1},$ and $O_{C2}$ are the centers of Napoleon's triangles for the other. It follows that triangles $O_{B2}O_{A2}O_{C1}$ and $O_{B1}O_{A1}O_{C2}$ are equilateral. In particular, say, $\angle O_{B2}O_{C1}O_{A2}=60^{\circ}.$ Since $O_{B2},$ $O_{A1},$ and $O_{A2}$ lie on the bisectors of angles at $C,$ $\angle O_{B2}O_{A1}O_{A2}=60^{\circ},$ making the four points $O_{B2},$ $O_{A1},$ $O_{C1},$ $O_{A2}$ concyclic. Similarly, points $O_{B1},$ $O_{A2},$ $O_{C2},$ $O_{A1}$ are also concyclic. But, by symmetry, so are points $O_{B2},$ $O_{B1},$ $O_{A1},$ $O_{A2}$ so that all six are.
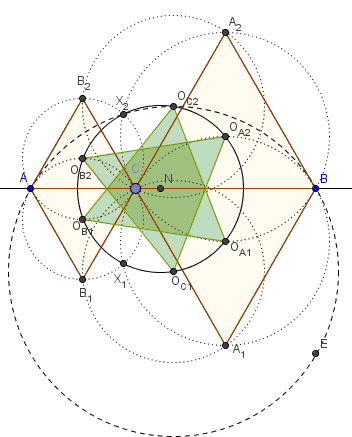
Now, quadrilateral $CO_{A2}X_2O_{B2}$ that consists of the centers of two circles and two points of their intersection, is symmetric with respect to the line of centers $O_{A2}O_{B2},$ implying $\angle O_{B2}X_2O_{A2}=\angle O_{B2}CO_{A2}=120^{\circ}.$ It follows that $\angle O_{B2}X_2O_{A2}=\angle O_{B2}O_{C1}O_{A2}=180^{\circ}$ and, therefore, four points $O_{B2},$ $X_2,$ $O_{A2},$ and $O_{A1}$ are concyclic adding $X_2$ (and similarly $X_1$) to the same circle.
Finally, $X_2$ is the intersection of the perpendicular bisectors of $CB_2$ and $CA_2$ which are the angles bisectors of $\angle CAB_2$ and $\angle CBA_2$ which do not depend on the position of $C.$ It follows that the circumcircle $(AO_{C2}B)$ also does not depend on the position of $C.$ Moreover, $\angle AO_{C2}B=120^{\circ},$ while $\angle AX_2B=\angle AX_2C +\angle CX_2B=60^{\circ}+60^{\circ}$ such that $\angle AX_2B=\angle AO_{C2}B,$ making four points $A,$ $X_2,$ $O_{C2},$ and $B$ concyclic.
An extra property $O_{A1}O_{B2}=O_{A2}O_{B1}=O_{C1}O_{C2}$ is left as an exercise.
Acknowledgment
The problem has been posted with solution by Dao Thanh Oai at the CutTheKnotMath facebook page.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73574088
