Problem 1, 2012 IMO

What is this about?

Problem

Given triangle $ABC,$ the point $J$ is the center of the excircle opposite the vertex $A.$ This excircle is tangent to the side $BC$ at $M,$ and to the lines $AB$ and $AC$ at $K$ and $L,$ respectively. The lines $LM$ and $BJ$ meet at $F,$ and the lines $KM$ and $CJ$ meet at $G.$ Let $S$ be the point of intersection of the lines $AF$ and $BC,$ and let $T$ be the point of intersection of the lines $AG$ and $BC.$

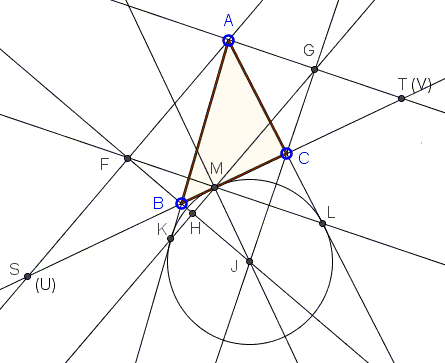
Problem 1, 2012 IMO

Prove that $M$ is the midpoint of $ST.$

Hint

The problem is discussed on an additional page. The solution there is quite different. Checking up the "Extra" button in the applet above, shows additional properties of the configuration and may suggest another solution.

Solution

The solution draws on the following diagram:

Problem 1, 2012 IMO

Let $AU\parallel KM,$ with $U\in BC;$ then triangles $BMK$ and $BUA$ are similar and, since $BM=BK$ we also have $BA=BU$ and, adding the two, $UM=AK.$

Similarly, for $V\in BC,$ with $AV\parallel LM,$ $VM=AL$. But $AK=AL$ so that $U=VM,$ making $M$ the midpoint of $UV.$ Now, $JB$ is the axis of symmetry of the isosceles trapezoid $AMKU$ (because $JC\perp KM$ and passes through its midpoint $H$) and so intersects $AU$ in its midpoint, say, $F'.$ It follows that $MF'$ is a midline in $\Delta UAV.$ In particular, $MF'\parallel AV.$ But by construction, $AV\parallel LM,$ implying that $F'\in LM,$ i.e., $F'=LM\cap JC=F.$ It follows that lines $AF$ and $AU$ coincide such that also $U=S.$ Similarly, $V=T,$ making $M$ the midpoint of $ST.$

Acknowledgment

The above solution is due to Leonard Giugiuc from Romania.

71536943