Pairing Monotone and Convex Functions
Problem
Solution 1
Since $g\,$ is convex, there is $u\in [a,b]\,$ such that on $[a,u]\,$ $g\,$ is nonincreasing and on $[u,b]\,$ $g\,$ is nondecreasing. If $u\in \{a,b\}\,$ then $g=0\,$ and the conclusion follows.
If $u\in (a,b)\,$ then there is a unique $c\in (a,b)\,$ such that $g\ge 0\,$ on $[a,c]\,$ and $g(x)\ge 0\,$ on $[c,b].\,$ Then, for $x\in [a,c],\,$ $f(x)-f(c)\le 0\,$ and $g(x)\le 0,\,$ so that $(f(x)-f(c))g(x)\ge 0,\,$ i.e. $f(x)g(x)\ge f(c)g(x),\,$ for $x\in [a,c].\,$ Similarly, $f(x)g(x)\ge f(c)g(x),\,$ for $x\in [c,b],\,$ and integrating the conclusion follows.
Solution 2
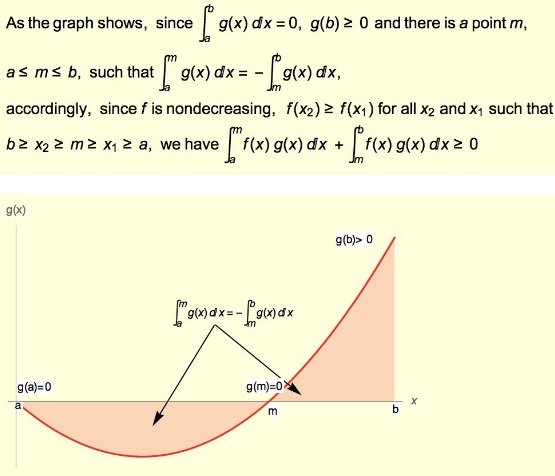
Acknowledgment
This problem has been kindly posted at the CutTheKnotMath facebook page by Leo Giugiuc, with a link to a solution by Gheorghe Duca at the mathematical inequalities facebook group. Solution 2 is by N. N. Taleb.
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73592463
