Find Minimum without Calculus
Problem
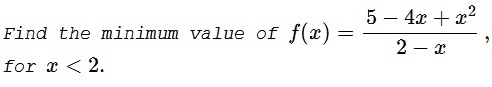
Solution 1
With the help of the AM-GM inequality,
$\displaystyle\begin{align} \frac{5-4x+x^2}{2-x} &= \frac{1+4-4x+x^2}{2-x}\\ &=\frac{1+(2-x)^2}{2-x}\\ &=\frac{1}{2-x}+(2-x)\\ &\ge 2, \end{align}$
since $2-x\gt 0.\,$ Now, equality is reached only when $2-x=\displaystyle\frac{1}{2-x},\,$ or, when $2-x=\pm 1.\,$ Only one of the choices falls into $(-\infty, 0):\,$ $2-x=1,\,$ i.e., $x=1.$
Solution 2
We can also reduce
$\displaystyle\frac{5-4x+x^2}{2-x} = \frac{(x-1)^2}{2-x}+2.$
Since the remining fraction is not negative $f(x)\ge 2.\,$ Obviously, $f(1)=2.$
Acknowledgment
Solution 1 is from the book below; Solution 2 is by Kamran Foroughi.
Reference
- Xiong Bin, Lee Peng Yee, Mathematical Olympiads in China (2009-2010). Problems and Solutions, World Scientific, 2013, #1
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73579418
