Integral of a Piece-wise Function
Problem

Solution
First of all, note that $h=g\circ f:\,[0,a]\rightarrow [0,c]\,$ is a continuous, surjective and strictly increasing function. In particular, $h(a)=c\,$ and $h^{-1}=f^{-1}\circ g^{-1}.\,$ We thus have to prove that
$\displaystyle\frac{1}{c}\int_0^ah^2(x)dx+\frac{1}{a}\int_0^c(h^{-1})^2(x)dx\le ac.$
Next we observe that $h(x)\le c\,$ and $h^{-1}(x)\le a\,$ and deduce that
$\displaystyle\frac{1}{c}\int_0^ah^2(x)dx+\frac{1}{a}\int_0^c(h^{-1})^2(x)dx\le \int_0^ah(x)dx+\int_0^ch^{-1}(x)dx.$
To this we apply the extreme case of Young's inequality that may be called Young's identity. The latter is illustrated by the diagram below:
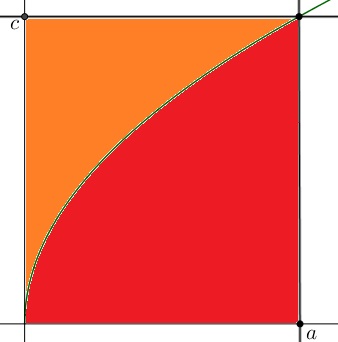
The red area represents $\displaystyle\int_0^ah(x)dx\,$ and the orange area represents $\displaystyle\int_0^ch^{-1}(x)dx.\,$ It follows that $\displaystyle\int_0^ah(x)dx+\int_0^ch^{-1}(x)dx=ac.$
Acknowledgment
The problem from the Romanian Mathematical Magazine (Problem #44) has been posted by Dan Sitaru at the CutTheKnotMath facebook page. Leo Giugiuc and Dan Sitaru commented with practically identical solutions.
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73578708
