Uniqueness of Number 5
Problem
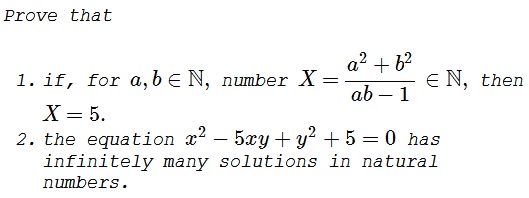
Solution 1 for the first part
The first problem is equivalent to showing that the equation
(1)
$x^2-qxy+y^2+q=0$
with $q\in\mathbb{N},$ has a solution $(x,y)\in\mathbb{N},$ if and only if $q=5.$
Obviously, for $q=1$ and for $q=2,$ (1) has no solution:
$x^2-xy+y^2+1=(x-y)^2+xy+1\gt 1\gt 0,\\ x^2-2xy+y^2+2=(x-y)^2+2\gt 0.$
Further, for no $q\gt 2,$ there is $x\in\mathbb{N},$ such that $(x,x)$ solves the equation. Indeed, for $x=y,$ (1) reduces to $x^2(2-q)+q=0,$ implying $\displaystyle x^2=\frac{q}{q-2}=1+\frac{2}{q-2},$ for $q\gt 2,$ which is impossible for integer $x$ because then $\displaystyle 1\lt\frac{q}{q-2}=1+\frac{2}{q-2}\le 3.$
Making a further step and fixing $y$ and $q$ we show that (1), as an equation in $x,$ cannot have a repeated root. Indeed, if the discriminant of the equation equals $0,$ i.e., if $y^2q^2-4(y^2+q)=0,$ then $\displaystyle y^2=\frac{4q}{q^2-4}.$ Since, for $q\gt 2,$ $\displaystyle \frac{4q}{q^2-4}$ is a decreasing function of $q,$ $\displaystyle y^2=\frac{4q}{q^2-4}\le\frac{12}{5}$ and is never $1$ because the equation $q^2-4q-4=0$ has no integer roots.
Now, from the quadratic formula, or Viète's theorem, as a quadratic equation in $x,$ (1) has either two integer roots or none.
For a fixed $q,$ let $y\gt 0$ be the least number for which (1) has positive integer solutions, say, $x=u$ and $x=v.$ Then, $u,v\gt y$ because if one of these is not true, we could swap $x$ and $y$ and get a solution of (1) with a smaller $y.$ So, assume $y\lt u\lt v,$ or $u\ge y+1$ and $v\ge y+2.$ Since $u+v=qy$ and $uv=y^2+q,$
$\begin{align}y^2+q-qy&=uv-u-v=(u-1)(v-1)-1\\ &\ge y(y+1)-1=y^2+y-1, \end{align}$
from which $1-y+q-qy\ge 0,$ i.e., $(1-y)(1+q)\ge 0.$ This is only possible if $y=1$ and all the inequalities are in fact equalities, implying $u=2,$ $v=3,$ $q=5$ (from (1).)
Solution 2 for the first part
Suppose $a\geq b$. First we treat a few special cases. Suppose $b\leq 3$. Then few calculations give the only solutions $(a,b)\in \{(2,1),(3,1),(9,2),(14,3)\}$, and in each solution we obtain $\displaystyle \frac{a^2+b^2}{ab-1}=5$. Also, $a=bk,k \in \mathbb{Z}$ gives solutions corresponding to $b=1$.
Therefore we may assume now $a > b\geq 4$ and $a=bk+l,0 < l < b; k,l\in \mathbb{Z}.$ Then
$\displaystyle \begin{align}\frac{a^2+b^2}{ab-1}&=\frac{abk+al+b^2}{ab-1}\\ &=k+\frac{al+b^2+k}{ab-1} \end{align}$
Note that
$\displaystyle\begin{align}al+b^2+k&\leq a(b-1)+b^2+a=ab+b^2\\ &=ab-2+b^2+2 \lt ab-2+b^2+b\\ &\leq ab-2+ab= 2(ab-1). \end{align}$
This implies $\displaystyle \frac{al+b^2+k}{ab-1} \lt 2$, hence $al+b^2+k=ab-1$. We have $a=bk+l$, so $bkl+l^2+b^2+k=b^2k+bl-1$, and
$\displaystyle \begin{align} k&=\frac{l^2+b^2-bl+1}{b^2-bl-1}\\ &=\frac{b^2+(b-l)^2}{b(b-l)-1}-1 \end{align}$
Therefore the problem for pair $(a,b)$ becomes the problem for the pair $(b,b-l)$. Since $b \lt a,b-l \lt b$, the sequence of pairs descends until we eventually reach $b_0-l_0\leq 3 $. In this case, as we know $\displaystyle \frac{b_0^2+(b_0-l_0)^2}{b_0(b_0-l_0)-1}=5,$ so $k=5-1=4,$ making $\displaystyle \frac{a_1^2+b_1^2}{a_1b_1-1}=k+1=5$. Going up we obtain that for initial $(a,b),$ $\displaystyle \frac{a^2+b^2}{ab-1}=5.$
Solution 1 for the second part
Thus consider the equation
(2)
$x^2-5xy+y^2+5=0.$
We already found two solutions - $(2,1)$ and $(3,1).$ By symmetry, we can add $(1,2)$ and $(1,3)$ but there are more. For every solution $(x,y),$ there is another solution with the same $y,$ viz., $(5y-x,y).$ Indeed,
$(5y-x)^2-5(5y-x)y+y+2=x^2-5xy+y^2=-5.$
Note that, if $y\gt x$ then $5y-x\gt 4y\gt y.$ It follows that any two successive terms of the sequences
$1,2,9,43,206,987,\ldots\\ 1,3,14,57,321,1538,\ldots,$
where every term is obtained from the previous two - $x$ and $y$ - from the formula $5y-x$ such that any two consecutive terms solve (2).
equalities, implying $u=2,$ $v=3,$ $q=5$ (from (1).)Solution 2 for the second part
With a fixed $y,$ the discriminant of (2) is $\Delta=21y^2-20.$ Let's find configurations in which $21y^2=k^2$ for an integer $k.$ In other words, let's find positive integers $k$ and $y$ such that $k^2-21y^2=-20.$ First remark that, with
$\displaystyle M=\left\{X=\left(\begin{array}{cc}a&b\\21b&a\end{array}\right):\,a,b\text{ integer}\right\},$
$(M,+,\cdot)$ is a commutative ring. Further, $\displaystyle A=\left(\begin{array}{cc}1&1\\21&1\end{array}\right)\in M$ and $\det A=-20.$ Also, $\displaystyle B=\left(\begin{array}{cc}55&12\\252&55\end{array}\right)\in M$ and $\det B=1.$ Thus, for any $n\ge 1,$ $AB^n\in M$ and $\det AB^n=-20.$
However,
$\displaystyle AB^n=\left(\begin{array}{cc}\,1&1\\21&1\end{array}\right)\left(\begin{array}{cc}\,a_n&b_n\\21b_n&a_n\end{array}\right)=\left(\begin{array}{cc}\,a_n+21b_n&a_n+b_n\\21(a_n+b_n)&a_n+21b^n\end{array}\right),$
implying that, for $n\ge 1,$, if $y=a_n+b_n$ and $k=a_n+21b_n,$ we have $y^2-20=k^2,$ and we are done.
Acknowledgment
This is problem $M1225^{*}$ from the Russian Kvant Magazine (n5, 1990). The problem is by S. Mamikonyan and G. Oganesyan. Solution 2 for the first part is by Bogdan Lataianu; Solution 2 for the second part is by Leo Giugiuc.
It was observed by Gary Davis that, the positive integers $b$ for which, for some positive integer $a,$ $\displaystyle \frac{a^2+b^2}{ab-1}$ is again a positiveve integer (necessarily $5)$ is the sequence A237254 in the online encyclopedia of integer sequences.
![]()
|Contact| |Up| |Front page| |Contents| |Arithmetic|
Copyright © 1996-2018 Alexander Bogomolny73582176
