Illustrated Sum of Cubes - All in a Plane
Problem
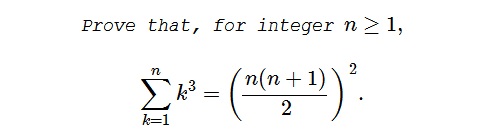
Solution 1
Let's denote the triangular numbers $\displaystyle t_k=\frac{k(k+1)}{2}$ and draw the graph of $y=2x,$ marking point $t_k$ on the $x-axis$ and points $2t_k$ on the $y-axis:$
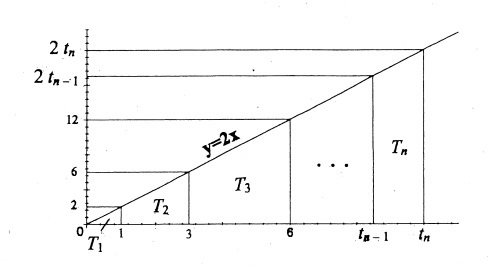
Joining the points to the graph by lines parallel to the axes creates below the graph regions $T_1,$ $T_2,$ and so on. All, except for the first one which is a triangle, are trapezoids.
Region $T_k$ is bounded by the $x-axis,$ the graph of $y=2x$ and two vertical lines $x=t_{k-1}$ and $x=t_k.$ If we set $t_0=0,$ the area $[T_k],$ $k\gt 0,$ is given by
$\displaystyle\begin{align}[T_k]&=\frac{1}{2}(2t_{k-1}+2t{k})(t_{k}-t_{k-1})=t^2_k-t^2_{k-1}\\ &=\frac{k^2(k+1)^2-(k-1)^2k^2}{4}=\frac{4k^3}{4}=k^3. \end{align}$
Thus, the area, say $A,$ of the triangle below the graph of $y=2x$ from the origin to $t_n$ is, on one hand,
$\displaystyle [T_1]+[T_2]+\ldots =\sum_{k=1}^n[T_k]=\sum_{k=1}^nk^3.$
On the other hand, it is equal to $\frac{1}{2}t_n\cdot 2t_n=t_n^2.$ Now we equate:
$\displaystyle 1^3+2^3+3^3+\ldots+n^2=(1+2+3+\ldots+n)^2=\left(\frac{n(n+1)}{2}\right)^2.$
Solution 2
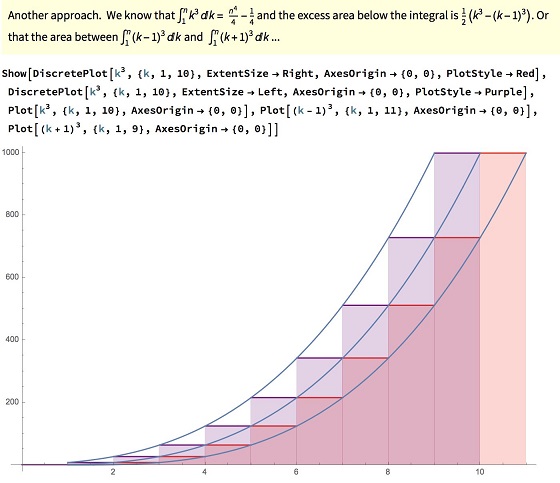
$n+1,$ $n-1$ for the band of integration. So $\displaystyle I(k)+\frac{1}{2}(I(k+1)-I(k-1)$ where $I(.)$ is the integral of $k^3$ and the upper limit is $n,$ $n-1,$ $n+1$ respectively.
Solution 3
The proof is by induction:
Let $P(n)$ be the statement that the required equality is true for some integer $n \ge 1$.
Base Case: $n = 1$:
$\displaystyle \begin{align} \sum_{k=1}^1 k^3 &= \left( {n(n+1) \over 2} \right)^2\\ &= \left( {1(1+1) \over 2} \right)^2 \Rightarrow 1 = 1 \end{align}$
Inductive Step: Suppose that $P(n)$ holds true. Now show that $P(n+1)$ also holds:
$\displaystyle \begin{align} \sum_{k=1}^{n+1} k^3 &= \sum_{k=1}^{n} k^3 + (n+1)^3\\ &= \left( {n(n+1) \over 2} \right)^2 + (n+1)^3 \\ &= (n+1)^2 \left[ \left( {n \over 2} \right)^2 + (n+1) \right] \\ &= {(n+1)^2 \over 4} \left[ n^2 + 4n + 4 \right] \\ \end{align}$
Thus $\displaystyle \sum_{k=1}^{n+1} k^3 = \left({(n+1)(n+2) \over 2}\right)^2$ so that $P(n+1)$ holds.
Solution 4
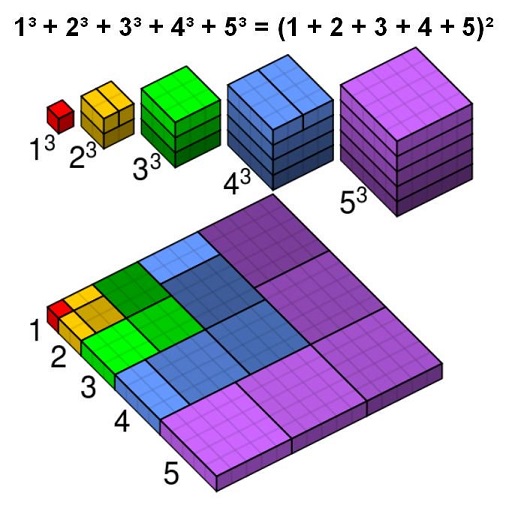
Acknowledgment
Solution 1 is one of the elegant pieces gracefully mailed to me by Sidney Kung. Other solutions came in response to my tweet announcement. Solution 2 is by N. N. Taleb; Solution 3 is by Gabriel Leitao; Solution 4 is is by Cmglee from the wikimedia commons. It was submitted by Vincent Pantaloni. This is a beautified version of a proof by J. Barry Love that was published in the Math Magazine (March 1977, v 50, n 2, p 74) and then reproduced in Proofs Without Words by Roger Nelson (MAA, 1993, p. 85).
There is also a page that introduces a general approach to summing power series.
![]()
|Contact| |Up| |Front page| |Contents| |Arithmetic|
Copyright © 1996-2018 Alexander Bogomolny73582124
