An Equation in Integers and Rational Numbers
Problem
Find all pairs of positive integers $x,y$ such that
$x^x = (x-y)^{x+y}.$
Solution
Assuming the equation solved, observe that every factor of the left-hand side divides the right-hand side. Thus, every factor of $x$ divides $x-y$ and, therefore, $y.$ Since, necessarily $x\gt y$ the converse is also true: every factor of $y$ divides $x,$ implying $x=ky,$ with integer $k$ (all factors of which are incidentally among the factors of $x$ and $y).$ Substituting this into the equation gives
$(ky)^{ky} = (ky-y)^{ky+y},$
or, after reduction,
$k^k = y(k-1)^{k+1}.$
Consider the graph of function $\displaystyle y=\frac{k^k}{(k-1)^{k+1}}:$
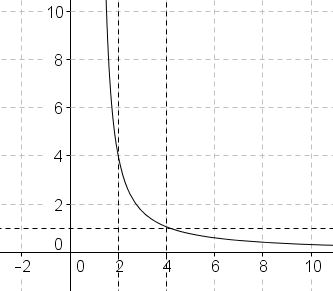
We are only interested in the integer values of $k$ that produce integer $y.$ There is only one such $k,$ viz., $k=2.$ ($3$ and $4$ may be also suspected but are easily verified to be unsuitable. For values beyond $4$ the function is less than $1).$
For $k=2,$ $y=4$ and $x=8.$ It is easily verified that $8^8=(8-4)^{8+4}.$
Rational solutions
The equation at hand is naturally reminiscent of the better known equation $x^y=y^x.$ In the integers, the latter has the solutions $(2,4)$ and $(4,2).$ However, interestingly it has infinitely many rational solutions. We may expect that the same is true of the given equation.
If $x$ and $y$ are rational so is $k.$ Assume $\displaystyle k=\frac{p}{q}$ in lower terms. $k^k = y(k-1)^{k+1}$ then reduces to
$\displaystyle y=\frac{q}{p}\left(1-\frac{q}{p}\right)^{-\frac{p+q}{q}}.$
As with the older equation, we conclude that a solution is only possible when $q=1,$ making
$\displaystyle y=p^{p}(p-1)^{-(p+1)}$ and $x=p^{p+1}(p-1)^{-(p+1)}.$
We van verify that $\displaystyle x^x=\left(\frac{p^{p+1}}{(p-1)^{p+1}}\right)^{\frac{p^{p+1}}{(p-1)^{p+1}}}=\left(\frac{p}{p-1}\right)^{(p+1)\frac{p^{p+1}}{(p-1)^{p+1}}}$ while
$\displaystyle x-y=\frac{p^{p+1}-p^{p}}{(p-1)^{p+1}}=\frac{p^{p}}{(p-1)^{p}}=\left(\frac{p}{p-1}\right)^{p}$
and
$\displaystyle x+y=\frac{p^{p+1}+p^{p}}{(p-1)^{p+1}}=\frac{p^{p}(p+1)}{(p-1)^{p+1}}$
which shows that, indeed, $x^x=(x-y)^{x+y}.$
Acknowledgment
The problem in integers has been posted by Bùi Quang Tuán at the CutTheKnotMath facebook page.
Remark
In the case of rational solutions, it is not as obvious as when the solutions are assumed to be integers, that $x=ky.$ This is left as an exercise.
![]()
|Contact| |Front page| |Contents| |Arithmetic|
Copyright © 1996-2018 Alexander Bogomolny73579164
