An Equation in Factorials
Problem
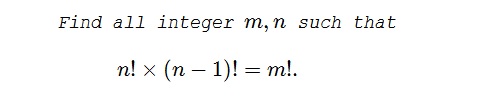
Lemma
For $N\gt 5$ there are at least two prime numbers $P,Q$ that satisfy $N\lt P,Q\lt 2N.$
In 1952, Jitsuro Nagura proved that for $N \ge 25,$ there is always a prime between $N$ and $\displaystyle \frac{6N}{5}.$ Since $\displaystyle \left(\frac{6}{5}\right)^3=1.728\lt 2$ it follows that in fact, for $N\ge 25,$ there are at least three primes between $N$ and $2N.$ For $N\gt 5,$ by inspection, there are at least two primes between $N$ and $2N$
Reference
Jitsuro Nagura (1952). "On the interval containing at least one prime number". Proc. Japan Acad. 28 (4): 177-181. doi:10.3792/pja/1195570997.
Solution 1
There are two obvious solutions $m=n=1$ and $m=n=2.$ Are there more?
$n!\times (n-1)!=n\cdot [(n-1)!]^2.$ Obviously, $n\lt m\lt 2n.$ Thus there is no solution if $m!$ has a non-square factor greater than $m.$ Now, for $m\gt 10$ there are always two primes, say $p$ and $q$ which are greater than $\displaystyle \frac{m}{2}$ but not greater than $m.$ Then
$\displaystyle pq\ge \left(\frac{m}{2}+\frac{1}{2}\right)\left(\frac{m}{2}+\frac{1}{2}+2\right)=\frac{m^2}{4}+\frac{6m}{4}+\frac{5}{4}\gt m,$
because the latter inequality is equivalent to $(m+1)^2+1\gt 0.$ We see that $pq$ is a non-square factor of $m!$ which is greater than $m.$ Hence, the given equation has no solution with $m\gt 10.$ By inspection, $7!\times 6!=10!.$
Solution 2
Let's suppose that there's an $m > 10$ s.t. $n!(n-1)!=m!$
Let $p$ and $q$ be the two biggest primes smaller than $m.$ Since they divide $m!,$ both $p$ and $q$ must divide $n!(n-1)!.$ At least one them - say $q$ - divides $(n-1)!.$ Hence $q^2$ divides $m!$
But by the lemma above, $\displaystyle q \gt \frac{m}{2},$ absurdum.
Acknowledgment
This is problem 66 from C. W. Trigg's Mathematical Quickies, Dover, 1985. For the life of me I am unclear why Trigg considered that problem as a Quickie.
Solution 2 is by Lorenzo Villa.
A twitter follower has observed that $n=1, m=0$ is another trivial solution.
|Contact| |Front page| |Contents| |Algebra| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73566832
