The Contest Corner Problem 210 from Crux
Problem
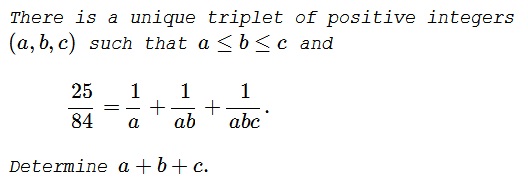
Solution 1
The equation is equivalent to $25abc=84(bc+c+1)$ which can be rewritten as
$(25a-84)(bc+c+1)=25a(c+1)$
and this implies $a\ge 4.\,$ Let's take $a=4$ and see what transpires. The equation reduces to $25bc=21(bc+c+1),\,$ or, $4bc=21(c+1)\,$ so that $\displaystyle b=\frac{21}{4}\cdot\frac{c+1}{c}\gt 5.$ This suggests taking $b=6$ and, from here, $c=7.$
The problem stipulates existence of a single triplet $(a,b,c),$ subject to the premises. Still, let's check that we do not get any other.
We began we choosing $a=4.\,$ Now, what if $a\ge 5?$ We would have then that
$\displaystyle b=\frac{84}{25a-84}\cdot\frac{c+1}{c}$
which is less than $2$ in contradiction with the requirement $a\le b.$
Thus $a=4,\,$ $b=6,\,$ $c=7$ and $a+b+c=17.$
Solution 2
We first find $a.$ Since $a\leq b \leq c,$
$\displaystyle \frac{1}{a}\lt \frac{25}{84}\leq\frac{1}{a}+\frac{1}{a^2}+\frac{1}{a^3}.$
The first inequality gives a lower bound on $a$ and indicates that integer $\displaystyle a\gt \frac{84}{25}=3.36.$
The second inequality gives an upper-bound on $a$ and indicates the integer $a\lt 4.32$ (value $4.32$ is the root if equality).
The only integer that satisfies both limits is $a=4.$ Plugging $a=4$ in the original equality yields:
$\displaystyle \frac{4}{21}=\frac{1}{b}+\frac{1}{bc}.$
Similar to finding $a,$ we have:
$\displaystyle \frac{1}{b}\lt \frac{4}{21}\leq\frac{1}{b}+\frac{1}{b^2}.$
Left inequality yields $b\gt 5.25$ and the second inequality yields $b\lt 6.1.$ The only integer in this range is $b=6.$
Now plugging $a=4$ and $b=6$ in the original equality, we find $c=7.$
So, the unique solution is $(a,b,c)=(4,6,7)$ yielding $a+b+c=17.$
Solution 3
Let $ b= a+\epsilon ,c=a+\xi +\epsilon, \epsilon, \xi \geq 0.$
$\displaystyle \begin{align} \lim_{\epsilon\to 0,\xi \to 0}\{a:\frac{25}{84}&=\frac{1}{a (a+\epsilon ) (a+\xi +\epsilon )}+\frac{1}{a (a+\epsilon )}+\frac{1}{a}\}\\ &=\small{\frac{1}{75}\left(3 \sqrt[3]{14 \left(25 \sqrt{22481}+5543\right)}+\sqrt[3]{2095254-9450 \sqrt{22481}}+84\right)}\\ & \approx 4.31, \end{align}$
and
$\displaystyle \lim_{\epsilon\to \infty,\xi \to \infty}\{a:\frac{25}{84}=\frac{1}{a (a+\epsilon ) (a+\xi +\epsilon )}+\frac{1}{a (a+\epsilon )}+\frac{1}{a}\}=\frac{84}{25}\approx 3.36,$
so $3.36 \leq a \leq 4.31,$ therefore $a=4$.
(We skip $\displaystyle \lim_{\epsilon\to \infty,\xi \to 0}$ and $\displaystyle \lim_{\epsilon\to 0,\xi \to \infty}$ as they will be interior.)
We need to find positive integers satisfying
$\displaystyle \frac{25}{84}=\frac{1}{4 (\epsilon +4) (\xi +\epsilon +4)}+\frac{1}{4 (\epsilon +4)}+\frac{1}{4}$
or
$\displaystyle \xi =\frac{-4 \epsilon ^2-11 \epsilon +41}{4 \epsilon -5}.$
For $\epsilon=2$, $\xi=1$ (we get by tinkering). So $a=4, b=6$, and $c=7$.
Solution 4
An Engel expansion of a positive rational number $x$ is a *nondecreasing* sequence $x_1\leq x_2 \leq ... \leq x_n$ of positive integers, such that
$\displaystyle x = \frac{1}{x_1} + \frac{1}{x_1x_2} + ... + \frac{1}{x_1x_2...x_n} =: \mathbf{R}(x_1,...,x_n).$
Note that
$\displaystyle \mathbf{R}(x_1,x_2,...,x_n) = \frac{1+\mathbf{R}(x_2,...,x_n)}{x_1}.$
Every positive rational number $x$ has a unique Engel expansion $\mathbf{S}(x) := (x_1,...,x_n)$.
I will skip the proof of uniqueness and give a procedure to compute $\mathbf{S}(x)$: Write $\displaystyle x = \frac{a}{b}.$
If $a = 0$, then $\mathbf{S}(x) = ()$, the empty sequence.
Otherwise our goal is to write $\displaystyle \mathbf{S}\frac{a}{b} = \left(x_i,\mathbf{S}\frac{a'}{b}\right))$, or in other words
$\displaystyle \frac{a}{b} = \frac{1+a'/b}{x_i} \;\Leftrightarrow\; ax_i = b+a'.$
Clearly we can choose $0 \leq a' \lt a$ such that $a$ divides $b+a'$ and then $\displaystyle x_i = \frac{b+a'}{a}.$
Remark: Because $a' \lt a$ the numerator keeps decreasing, and the sequence eventually terminates after at most $a$ steps.
Let's apply this to $x = 25/84$.
$\displaystyle \begin{align} &a = 25, b = 84 = 3a + 9 \,\Rightarrow\, a' = 16\text{ and }x_1 = \frac{84 + 16}{25} = 4\\ &a = 16, b = 84 = 5a + 4 \,\Rightarrow\, a' = 12\text{ and }x_2 = \frac{84 + 12}{16} = 6\\ &a = 12, b = 84 = 7a \,\Rightarrow\, a' = 0\text{ and }x_3 = \frac{84+0}{12} = 7\\ &a = 0, \end{align}$
we're done.
Therefore $\displaystyle \frac{25}{84} = \mathbf{R}(4,6,7)$.
Solution 5
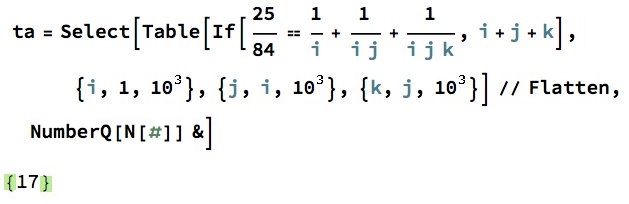
Solution 6
$\displaystyle \frac{25}{84}=\frac{1}{a b c}+\frac{1}{a b}+\frac{1}{a}$
Using the Greedy Algorithm for the Egyptian fraction $\displaystyle \frac{25}{84}$, updated as follows:
$\displaystyle \frac{x}{y}=\frac{1}{\left\lceil \frac{y}{x}\right\rceil }+\frac{- y \text{ mod }x}{ y\left\lceil \frac{y}{x}\right\rceil }$
First pass:
$\displaystyle \frac{25}{84}=\frac{1}{4}+\frac{1}{21}$
For the second pass, we need $\displaystyle \frac{1}{21}=\frac{1}{4 b }+\frac{1}{4 b c}$.
We note that the Fibonacci trick for $n$ steps allows us to assert that the $n$ fractions are unique for $n$ Egyptian fractions.
Second pass:
$\displaystyle \frac{4}{21}=\frac{1}{6}+\frac{1}{42}$
So
$\displaystyle \frac{25}{84}=\frac{1}{4}+\frac{1}{4 \times 6}+\frac{1}{4\times 6\times 7}$
Acknowledgment
This strange problem comes from the Contest Corner of the Canadian Crux Mathematicorum, problem CC210. It could be understood as the request to find $a+b+c$ without first finding individual values of $a,b,c.$ No progress was made in attempts to perform this feat. Solution 2 above is by Faryad D. Sahneh; Solutions 3, 5 and 6 are by N. N. Taleb; Solution 4 is by Long Huynh Huu, with thanks to Faryad D. Sahneh for identifying a link to the definition of Engel expansion.
![]()
|Contact| |Up| |Front page| |Contents| |Arithmetic|
Copyright © 1996-2018 Alexander Bogomolny73576865
