On the Intersection of 1+x and e^x and Trigonometric Consequences
Problem
Find all $x\in (0,2\pi )$ such that
$\displaystyle e^{\sin x-\cos x}=\tan x.$
Hint 1
It's never a bad idea to sketch the graphs of the two sides of a functional equation. Here's in the case at hand two graphs with different scales on $x$-axis:
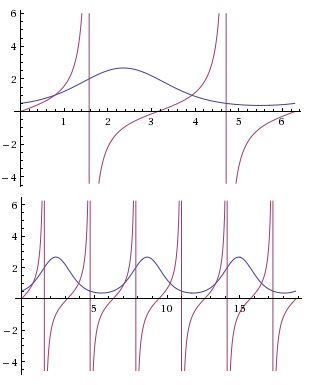
Hint 2
It is clear that on the interval $(0,2\pi )$ the graphs of $y=e^{\sin x-\cos x}$ and $y=\tan x$ intersect twice. It is less obvious that this relates to the fact that $y=2^x$ and $y=1+x$ (the former being a concave function and, therefore, the region above the graph $y=2^x$ is convex) have just two intersections:
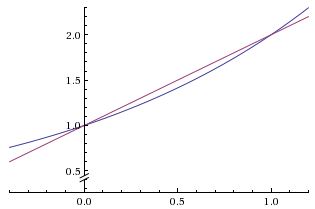
The two graphs intersect at $x=0$ and $x=1$ such that in-between $2^x\gt 1+x$ while outside the interval $(0,1)$ $2^x\lt 1+x.$
Solution
Assuming $x\in (0,2\pi),$ set $a=\sin x$ and $b=\cos x$ so that $\displaystyle\tan x=\frac{b}{a}.$ We have to consider several cases:
-
$\displaystyle x\in \left(0,\frac{\pi}{4}\right).$ $1\gt b\gt a\gt 0.$ It follows that $-1\lt a-b\lt 0,$ implying $\displaystyle e^{a-b}\gt 1+(a-b)\gt \frac{a}{b}.$ To see that the latter inequality holds observe that it is equivalent to $\displaystyle\frac{1}{b}(b-a)(1-b)\gt 0.$ Thus, for $\displaystyle x\in \left(0,\frac{\pi}{4}\right),$ $\displaystyle e^{\sin x-\cos x}\gt\tan x.$
-
$\displaystyle x\in \left(\frac{\pi}{4},\frac{\pi}{2}\right).$ $1\gt a\gt b\gt 0.$ It follows that $0\lt a-b\lt 1,$ implying $\displaystyle e^{a-b}\gt 1+(a-b)\lt \frac{a}{b}.$ To see that the latter inequality holds observe that it is equivalent to $\displaystyle\frac{1}{b}(b-a)(1-b)\lt 0.$ Thus, for $\displaystyle x\in \left(\frac{\pi}{4},\frac{\pi}{2}\right),$ $\displaystyle e^{\sin x-\cos x}\lt\tan x.$
The above gives one solution $\displaystyle x=\frac{\pi}{4}.$
There is no solution in $\displaystyle x\in \left(\frac{\pi}{2},\pi\right)$ where $\sin x$ and $e^{\sin x-\cos x}$ are positive while $\cos x$ and $\tan x$ are negative. Then there is a solution $\displaystyle x=\frac{5\pi}{4}$ in the third quadrant and no solutions in the fourth one.
Generalization
The solutions to the original equation are attained at $x$ for which $\sin x=\cos x,$ so that both $e^{\sin x-\cos x}$ and $\tan x$ equal $1.$
These same $x$ solve the whole families of equations $(n\ge 1):$$\displaystyle e^{\sin^{n} x-\cos^{n} x}=\tan^{n} x.$
and
$\displaystyle e^{\sin^{n} x-\cos^{n} x}=\tan x.$
As a hint, below are the graphs with $n=2$ for the second and first case (in this order.)
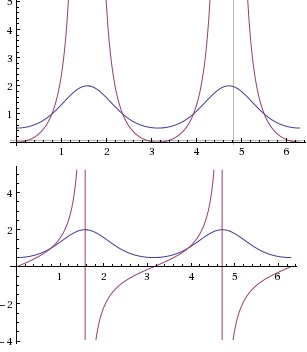
Second solution
The function $\displaystyle f(x)=\frac{e^x}{x}$ is decreasing and negative on $[-1,0),$ decreasing and positive on $(0,1].$
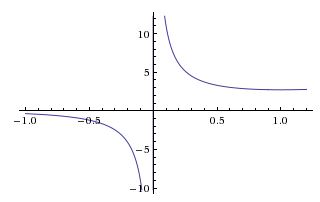
Thus $\displaystyle\frac{e^u}{u}=\frac{e^v}{v},$ with $u = \sin x,$ and $v = \cos x,$ is possible if and only if $u = v.$
(It can be verified that $\displaystyle f'(x)=\frac{(x-1)2^{x}}{x^2}\lt 0$ on $[-1,0)\cup (0,1]).$
For Extra Credit
Solving $\displaystyle a^{\sin^{n} x-\cos^{n} x}=\tan^{n} x,$ $\displaystyle a\in [\frac{1}{e},1)\cup (1,e])$ is practically the same as the above.
Acknowledgment
This is a problem from Dan Sitaru's book "Math Accent" that was posted, along with the solution, by Leo Giugiuc at the CutTheKnotMath facebook page. The second solution has been posted by Grégoire Nicollier in the comments area below and by Cristinel Mortici at the CutTheKnotMath facebook page. Dan Sitaru, Cristenel Mortici, Leo Giugiuc get extra credit for expanding the original problems to solving $\displaystyle a^{\sin^{n} x-\cos^{n} x}=\tan^{n} x.$
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73578352
