Solving a Peculiar Third Degree Equation
Statement
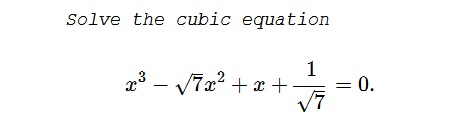
Solution
Define $\displaystyle a=\cot\frac{\pi}{7},$ $\displaystyle b=\cot\frac{2\pi}{7},$ $\displaystyle c=\cot\frac{4\pi}{7}.$ Observe that $a,b\gt 0,$ while $c\lt 0.$ However, since $\displaystyle \frac{\pi}{7},\frac{2\pi}{7},\frac{4\pi}{7}\gt 0$ and $\displaystyle \frac{\pi}{7}+\frac{2\pi}{7}+\frac{4\pi}{7}=\pi,$ then $a+b\gt 0,$ $b+c\gt 0$ and $c+a\gt 0,$ implying that also $a+b+c\gt 0.$ Moreover, $ab+bc+ca=1.$
Consider the polynomial of degree $6:$
$\displaystyle P(x)=\frac{(x+i)^7-(x-i)^7}{2i}=7x^6-35x^4+21x^2-1.$
Now, since $\displaystyle e^{i\frac{k\pi}{7}}$ are the $7^{th}$ roots of unity, $P(x)$ has six roots:
$\displaystyle \cot\frac{\pi}{7}=a,\cot\frac{2\pi}{7}=b,\cot\frac{3\pi}{7}=-\cot\frac{4\pi}{7}=-c,\\ \displaystyle \cot\frac{4\pi}{7}=c,\cot\frac{5\pi}{7}=-\cot\frac{2\pi}{7}=-b,\cot\frac{6\pi}{7}=-\cot\frac{\pi}{7}=-a.$
We my thus conclude that the roots of the cubic polynomial $Q(x)=7x^3-35x^2+21x-1$ are $a^2,$ $b^2,$ $c^2.$
By Viète's theorem, $\displaystyle a^2b^2c^2=\frac{1}{7}.$ So that $\displaystyle abc=-\frac{1}{\sqrt{7}}.$ Further, $a^2+b^2+c^2=5,$ implying
$(a+b+c)^2=a^2+b^2+c^2+2(ab+bc+ca)=7$
and, since $a+b+c\gt 0,$ $a+b+c=\sqrt{7}.$ Again, with a reference to Viète's theorem, $a,b,c$ serve as the roots of the given equation, $\displaystyle x^3-\sqrt{7}x^2+x+\frac{1}{\sqrt{7}}=0.$
Acknowledgment
Leo Giugiuc has kindly communicated to me the problem, along with a solution of his.
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73512133
