A System of Two Equations Replete with Squares
Problem
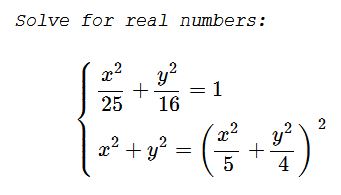
Solution
Let, for simplicity, $a=x^2,\,b=y^2.\,$ The system can be written as
$\displaystyle \left\{\begin{align}&16a+25b=400\\&a+b=\frac{(4a+5b)^2}{400}\end{align}\right.$
The second equation transforms into $400(a+b)=(4a+5b)^2.\,$ Replacing $400\,$ from the first equation gives
$(16a+25b)(a+b)=(4a+5b)^2,$
i.e.,
$16a^2+25ab+16ab+25b^2=16a^2+40ab+25b^2,$
which simplifies to $ab=0,\,$ same as $xy=0.\,$ Note that $x,y\,$ can't vanish simultaneously. Thus, two cases: either $x=0\,$ or $y=0.\,$ The first case gives solutions $(0,\pm 4),\,$ the second $(\pm 5, 0).$
Acknowledgment
Dan Sitaru has kindly posted the above problem of his from the Romanian Mathematical Magazine at the CutTheKnotMath facebook page, along with the above solution by Seyran Ibrahimov.
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73549658
