An Incidental Sum of 20

Assume to the contrary that the numbers are all distinct; WLOG, $x_1\lt x_2\lt\ldots\lt x_{144}.$ Then surely, for $k=1,\ldots, 144$ $x_k\gt k.$ It follows that, by telescoping at the last step,

$\displaystyle\begin{align}\sum_{k=1}^{144}\frac{1}{\sqrt{x_k}}&\lt \sum_{k=1}^{144}\frac{1}{\sqrt{k}}\\ &\lt\sum_{k=1}^{144}\frac{2}{\sqrt{k}+\sqrt{k-1}}\\ &=\sum_{k=1}^{144}2(\sqrt{k}-\sqrt{k-1})=2\sqrt{144}=24. \end{align}$

That's a contradiction. Hence, the numbers cannot be all distinct.

On the other hand, it is interesting to exhibit such a collection of integers.

First, observe that there exists a solution if some integers are allowed to be equal. One possible combination is $x_1=x_2=\cdots =x_{144}=36$.

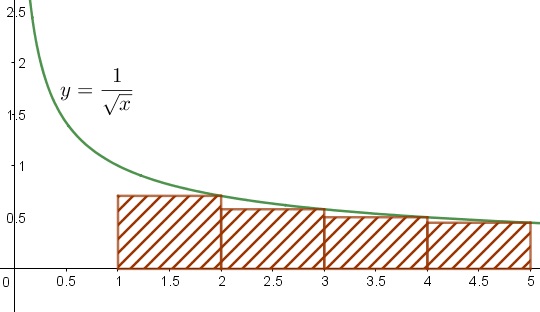
Suppose, there exists a solution when no two $x_i's$ are equal. Thus,

$\begin{equation*} 24=\sum_{i=1}^{144}\frac{1}{\sqrt{x_i}}\leq \sum_{i=1}^{144}\frac{1}{\sqrt{i}} \leq 1+\int_{x=1}^{144}\frac{dx}{\sqrt{x}}=23. \end{equation*}$

This is a contradiction. Therefore, our supposition cannot be true. We have shown that a solution exists and than no solution can have all positive integers distinct. Hence, all solutions have at least two integers equal.

The sum of the first $144$ integers (with the largest reciprocals) becomes $\displaystyle \sum_{k=1}^{144}\frac{1}{\sqrt{k}}\approx 22.58.$ Integers beyond $144$ do noot help as their reciprocals are two small. Therefore, we must pick one from the existing list $\{1,2,\ldots,144\}.$

This is a slight modification of a problem 8 from 's Mathematical Miniatures by S. Savchev and T. Andreescu (MAA, 2003, 121-122)

Solution 2 is by Amit Itagi; Solution 3 is by N. N. Taleb.