Scalar Product Optimization
Problem
Let $x,\;y,\;a,\;b$ be real numbers such that $(x+1)^2+y^2=1$ and $(a-2)^2+b^2=4.$ Find the extreme values of the expression $ax+by.$
Solution 1
The minimum is $-8$ because the two given circles are externally tangent at the origin and $ax+by$ is the scalar product of two vectors with the end points on the circles. Hence $2*4*(-1)=-8.$
To determine the maximum, consider the points $A(x,y),$ $B(a,b),$ and $O(0,0).$ Note that
$ax+by=\overrightarrow{OA}\cdot \overrightarrow{OB}=OA\cdot OB\cdot\cos\angle AOB.$
Hence, to achieve maximum, it is necessary that $A$ and $B$ lie on the corresponding circles. Observe also that $\angle AOB$ has to be acute which allows us to assume that the two points are in the upper half-plane. Thus, $A=(-1+\cos u,\;\sin u)$ and $B=(2+2\cos t,\;2\sin t),$ with $0\lt t,\; u\lt\pi.$ Setting $v=\angle AOB,$ we get on one hand
$\displaystyle\frac{A-O}{B-O}=\frac{OA}{OB}(\cos v+i\sin v)$
while, on the other,
$\displaystyle\begin{align} \frac{A-O}{B-O}&=\frac{-1\cos u+i\sin u}{2+2\cos t+2i\sin t}\\ &=\frac{i\sin\frac{u}{2}(\cos\frac{u}{2}+i\sin\frac{u}{2})}{2\cos\frac{t}{2}(\cos\frac{t}{2}+i\sin\frac{t}{2})}\\ &=\frac{\sin\frac{u}{2}}{2\cos\frac{t}{2}}\left(\cos\frac{\pi+u-t}{2}+i\sin\frac{\pi+u-t}{2}\right). \end{align}$
Since $\displaystyle\frac{\sin\frac{u}{2}}{2\cos\frac{t}{2}}\gt 0,$ we may identify the angles: $\displaystyle v=\frac{\pi +u-t}{2}$ and so $\displaystyle \cos v=\sin\frac{t-u}{2},$ implying, in particular, that $t\gt u.$ Substituting,
$\displaystyle\begin{align} ax+by&=OA\cdot OB\cdot\cos v=8\sin\frac{u}{2}\cos\frac{t}{2}\sin\frac{t-u}{2}\\ &=8\sin\frac{u}{2}\sin\frac{\pi- t}{2}\sin\frac{t-u}{2}. \end{align}$
But, $\displaystyle 0\lt \frac{u}{2},\;\frac{\pi-t}{2},\;\frac{t-u}{2}$ and $\displaystyle\frac{u}{2}+\frac{\pi-t}{2}+\frac{t-u}{2}=\frac{\pi}{2}.$ By Jensen's inequality,
$\displaystyle 8\sin\frac{u}{2}\sin\frac{\pi- t}{2}\sin\frac{t-u}{2}\le 1.$
For equality we need $u=60^{\circ}$ and $t=120^{\circ}.$
Solution 2
Note first that the problem could be generalized. Indeed, assuming that $x,\;y,\;a,\;b$ satisfy $(x+r)^2+y^2=r^2$ and $(a-s)^2+b^2=s^2,$ $(r,\; s\gt 0),$ $ax+by=rs(\cos v+i\sin v),$ and, at the extremes of this expression, angle $v$ is the same, independent of the radii $r,\; s$ of the circles. So, below I shall assume $r=s=1$ and use the same notations $A,\; B,\; O$ as in the first solution. Let $P(-1,0)$ and $Q(1,0)$ be the centers of the two circles
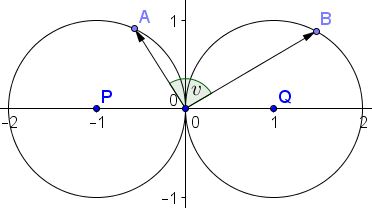
For a fixed point $B(a,b),$ the scalar product $ax+by$ is constant on straight lines perpendicular to $\overrightarrow{OB}.$ The maximum value (for a given $B)$ is attained for the line tangent to $(x+1)^2+y^2=1.$ If $A$ is the point of tangency, $PA$ is perpendicular to that line and, therefore, parallel to $OB.$
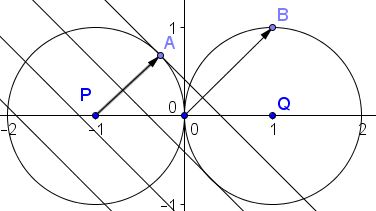
It follows that, if $A=(-1+\cos u,\;\sin u)$ then $B=(1+\cos 2u,\;\sin 2u):$
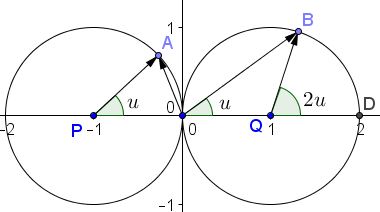
It then follows that
$\begin{align} ax+by&=(-1+\cos u)(1+\cos 2u)+\sin u\sin 2u\\ &=-1+\cos u-\cos 2u+(\cos 2u\cos u+\sin 2u\sin u)\\ &=-1+\cos u - (2\cos^2 u-1)+\cos u\\ &=-2\cos^2 u+2\cos u\\ &=-2\cos u(\cos u-1). \end{align}$
The parabola $f(t)=-2t(t-1)$ attains it maximum for $\displaystyle t=\frac{1}{2}.$ Therefore, the maximum of $ax+by$ is attained when $\displaystyle\cos u=\frac{1}{2},$ i.e., at $u=60^{\circ},$ implying $2u=120^{\circ},$ and also $v=60^{\circ}.$
With these, the maximum of $ax+by$ equals $\displaystyle\frac{1}{2},$ or in the general case, $\displaystyle\frac{rs}{2}.$ The minimum is rather obviously $(-2r)(2s)=-4rs.$
Acknowledgment
The problem has been posted by Leo Giugiuc at the CutTheKnotMath facebook page, followed by the solution by Claudia Nanuti, Diana Trailescu, Dan Sitaru and Leo Giugiuc (Solution 1).
|Up| |Contact| |Front page| |Contents| |Algebra| |Generalization|
Copyright © 1996-2018 Alexander Bogomolny
73579561
