Sam Walters' Four Questions

Observe that $\displaystyle Z^n-1=\prod_{k=0}^{n-1}(Z-z^k),$ so that $\displaystyle \frac{Z^n-1}{Z-1}=\prod_{k=1}^{n-1}(Z-z^k).$ From here,

$\displaystyle n=\lim_{Z\to 1}\frac{Z^n-1}{Z-1}=\lim_{Z\to 1}\prod_{k=1}^{n-1}(Z-z^k)=\prod_{k=1}^{n-1}(1-z^k).$

From $\displaystyle \frac{Z^n-1}{Z-1}=\prod_{k=1}^{n-1}(Z-z^k)$ we have $\displaystyle \sum_{k=0}^{n-1}Z^k=\prod_{k=1}^{n-1}(Z-z^k).$ Letting $Z=1$ proves $\displaystyle \prod_{k=1}^{n-1}(1-z^k)=n.$

$\displaystyle z=\cos \left(\frac{2 \pi }{n}\right)+i \sin \left(\frac{2 \pi }{n}\right)=e^{\frac{2 i \pi }{n}}$

$\displaystyle f=\prod _{k=1}^{n-1} \left(1-z^k\right)=\left(e^{\frac{2 i \pi }{n}};e^{\frac{2 i \pi }{n}}\right)_{n-1}$

where $\left(.,.\right)_{n-1}$ is the Q-Pochhammer function.

Since $(a;q)_{n-1}=\sum _{k=0}^{n-1} (-a)^k q^{{k\choose 2}} {n-1\choose k}_q$, where ${n-1\choose k}_q$ is the Q-Binomial function:

$\displaystyle f= \sum_{k=0}^{n-1}\left(-e^{\frac{2 i \pi }{n}}\right)^k \left(e^{\frac{2 i \pi }{n}}\right)^{\frac{1}{2} (k-1) k} {n-1\choose k}_{e^{\frac{2 i \pi }{n}}}$

Each summand equals 1, so $f=n$. As an illustration, for $n=7$:

$\displaystyle \begin{array}{l} 1 \\ -e^{-\frac{2 i \pi }{7}}-e^{\frac{2 i \pi }{7}}-e^{-\frac{4 i \pi }{7}}-e^{\frac{4 i \pi }{7}}-e^{-\frac{6 i \pi }{7}}-e^{\frac{6 i \pi }{7}}=1 \\ 3+2 e^{-\frac{2 i \pi }{7}}+2 e^{\frac{2 i \pi }{7}}+2 e^{-\frac{4 i \pi }{7}}+2 e^{\frac{4 i \pi }{7}}+2 e^{-\frac{6 i \pi }{7}}+2 e^{\frac{6 i \pi }{7}}=1 \\ -2-3 e^{-\frac{2 i \pi }{7}}-3 e^{\frac{2 i \pi }{7}}-3 e^{-\frac{4 i \pi }{7}}-3 e^{\frac{4 i \pi }{7}}-3 e^{-\frac{6 i \pi }{7}}-3 e^{\frac{6 i \pi }{7}}=1 \\ 3+2 e^{-\frac{2 i \pi }{7}}+2 e^{\frac{2 i \pi }{7}}+2 e^{-\frac{4 i \pi }{7}}+2 e^{\frac{4 i \pi }{7}}+2 e^{-\frac{6 i \pi }{7}}+2 e^{\frac{6 i \pi }{7}}=1 \\ -e^{-\frac{2 i \pi }{7}}-e^{\frac{2 i \pi }{7}}-e^{-\frac{4 i \pi }{7}}-e^{\frac{4 i \pi }{7}}-e^{-\frac{6 i \pi }{7}}-e^{\frac{6 i \pi }{7}}=1 \\ 1 \\ \end{array}$

$\displaystyle \begin{align} I&=\sum_{k=1}^{n-1}\frac{1}{1-z^k}=\sum_{k=1}^{n-1}\frac{z^{n-k}}{z^{n-k}-1}\\ &=\sum_{k=n-1}^{1}\frac{z^k}{z^k-1}=-\sum_{k=1}^{n-1}\frac{z^k}{1-z^k}. \end{align}$

It follows that

$\displaystyle \begin{align} 2I&=\sum_{k=1}^{n-1}\frac{1}{1-z^k}-\sum_{k=1}^{n-1}\frac{z^k}{1-z^k}\\ &=\sum_{k=1}^{n-1}\frac{1-z^k}{1-z^k}=\sum_{k=1}^{n-1}1=n-1. \end{align}$

Finally, $\displaystyle I=\sum_{k=1}^{n-1}\frac{1}{1-z^k}=\frac{n-1}{2}.$

For any $\alpha,$

$\displaystyle\begin{align}\frac{1}{1-e^{i\alpha}}+\frac{1}{1-e^{-i\alpha}}&=\frac{1}{1-e^{i\alpha}}+\frac{e^{i\alpha}}{e^{i\alpha}-1}\\ &=\frac{1-e^{i\alpha}}{1-e^{i\alpha}}=1. \end{align}$

If $n$ is odd, then, by pairing the conjugate expressions, we get immediately $\displaystyle \sum_{k=1}^{n-1}\frac{1}{1-z^k}=\frac{n-1}{2}.$ If $n$ is even, say, if $n=2m,$ then

$\displaystyle \begin{align}\sum_{k=1}^{n-1}\frac{1}{1-z^k}&=\sum_{k=1,k\ne m}^{2m-1}\frac{1}{1-z^k}+\frac{1}{1-z^m}\\ &=(m-1)+\frac{1}{2}=\frac{n}{2}-1+\frac{1}{2}=\frac{n-1}{2},\end{align}$

because $z^m=-1.$

As before, $\displaystyle \sum_{k=0}^{n-1}Z^k=\prod_{k=1}^{n-1}(Z-z^k).$ Differentiating both sides gives

$\displaystyle \sum_{k=1}^{n-1}kZ^{k-1}=\left[\prod_{k=1}^{n-1}(Z-z^k)\right]\cdot\left[\sum_{k=1}^{n-1}\frac{1}{Z-z^k}\right].$

Letting $Z=1$ and recollecting from the first question that $\displaystyle \prod_{k=1}^{n-1}(1-z^k)=n,$

$\displaystyle\sum_{k=1}^{n-1}\frac{1}{1-z^k}=\frac{1}{n}\sum_{k=1}^{n-1}k=\frac{n-1}{2}.$

We have

$\displaystyle \sum _{k=1}^{\infty} \frac{1}{1-z^k}=\frac{\psi _{1/z}^{(0)}(1)+\log(z-1)+\log(1/z)}{\log (z)}$

where $\psi _{1/z}^{(0)}(1)$ is the q-digamma function.

(The $q$-polygamma functions of order $m$, $\psi_q^{(m)}$, are analogues of the polygamma function defined by

$\displaystyle \psi_q^{(m)}(z)=\dfrac{\partial^m}{\partial z^m} \psi_q(z),$

where $\displaystyle \psi_q(z) = \dfrac{1}{\Gamma_q(z)} \dfrac{\partial}{\partial z} \Gamma_q(z).$ Here the function $\Gamma_q$ is the q-Gamma function. See functionwiki.)

$\displaystyle f_2=\sum _{k=1}^{n-1} \frac{1}{1-z^k}=-\frac{\psi _{z}^{(0)}(n)}{\log (z)}+n+\frac{\psi _{z}^{(0)}(1)}{\log (z)}-1$

We have

$\displaystyle f_2=\frac{i n \left(\psi _{e^{\frac{2 i \pi }{n}}}^{(0)}(n)-\psi _{e^{\frac{2 i \pi }{n}}}^{(0)}(1)\right)}{2 \pi }+n-1$

and can show that

$\psi _{e^{\frac{2 i \pi }{n}}}^{(0)}(n)-\psi _{e^{\frac{2 i \pi }{n}}}^{(0)}(1)=\frac{(n-1)}{n} i \pi$

Illustration:

$\displaystyle \begin{array} \,n=2,&\displaystyle f_2= -\frac{i \psi _{-1}^{(0)}(1)}{\pi }+\frac{i \psi _{-1}^{(0)}(2)}{\pi }+1=\frac{1}{2} \\ n=3,&\displaystyle f_2= -\frac{3 i \psi _{e^{\frac{2 i \pi }{3}}}^{(0)}(1)}{2 \pi }+\frac{3 i \psi _{e^{\frac{2 i \pi }{3}}}^{(0)}(3)}{2 \pi }+2 =1\\ n=4,&\displaystyle f_2= -\frac{2 i \psi _i^{(0)}(1)}{\pi }+\frac{2 i \psi _i^{(0)}(4)}{\pi }+3 =\frac{3}{2}\\ n=5,&\displaystyle f_2= -\frac{5 i \psi _{e^{\frac{2 i \pi }{5}}}^{(0)}(1)}{2 \pi }+\frac{5 i \psi _{e^{\frac{2 i \pi }{5}}}^{(0)}(5)}{2 \pi }+4 =2\\ n=6,&\displaystyle f_2= -\frac{3 i \psi _{e^{\frac{i \pi }{3}}}^{(0)}(1)}{\pi }+\frac{3 i \psi _{e^{\frac{i \pi }{3}}}^{(0)}(6)}{\pi }+5=\frac{5}{2} \\ \ldots=&\displaystyle f_2=\frac{n-1}{2} \end{array}$

To start with, note that

$\displaystyle \sum_{k=1}^{n-1}\frac{1}{(1-z^k)^2}=\sum_{k=1}^{n-1}\frac{z^{2k}}{(1-z^k)^2}.$

Using that we have

$\displaystyle\begin{align}n-1 &=\sum_{k=1}^{n-1}\frac{(1-z^k)^2}{(1-z^k)^2}\\ &=2\sum_{k=1}^{n-1}\frac{1}{(1-z^k)^2}-2\sum_{k=1}^{n-1}\frac{z^k}{(1-z^k)^2} \end{align}$

such that

$\displaystyle\begin{align} \sum_{k=1}^{n-1}\frac{1}{(1-z^k)^2}&=\frac{n-1}{2}+\sum_{k=1}^{n-1}\frac{z^k}{(1-z^k)^2}\\ &=\frac{n-1}{2}+\sum_{k=1}^{n-1}\frac{1}{(z^{-\frac{k}{2}}-z^{\frac{k}{2}})^2}\\ &=\frac{n-1}{2}+\sum_{k=1}^{n-1}\frac{1}{(2i\sin\left(\frac{\pi k}{n}\right))^2}\\ &=\frac{n-1}{2}-\frac{1}{4}\sum_{k=1}^{n-1}\frac{1}{\sin\left(\frac{\pi k}{n}\right))^2}\\ &=\frac{n-1}{2}-\frac{1}{4}\cdot\frac{n^2-1}{3}\\ &=-\,\frac{(n-1)(n-5)}{12}. \end{align}$

Truth be told, to derive $\displaystyle \sum_{k=1}^{n-1}\frac{1}{\sin\left(\frac{\pi k}{n}\right))^2}=\frac{n^2-1}{3}$ I have availed myself from the powerful wolframalpha.

We start with $\displaystyle \frac{\displaystyle \sum_{k=1}^{n-1}kZ^{k-1}}{\displaystyle \sum_{k=0}^{n-1}Z^k}=\sum_{k=1}^{n-1}\frac{1}{Z-z^k}.$ To simplify the typesetting, let $\displaystyle f(Z)=\sum_{k=1}^{n-1}kZ^{k-1}$ and $\displaystyle g(Z)=\sum_{k=0}^{n-1}Z^k.$ Obviously, $g'=f.$ Thus, we have $\displaystyle \frac{f}{g}=\sum_{k=1}^{n-1}\frac{1}{Z-z^k}$ which we differentiate:

$\displaystyle J=\sum_{k=1}^{n-1}\frac{1}{(Z-z^k)^2}=-\frac{f'g-fg'}{g^2}.$

Note that $\displaystyle J(1)=\sum_{k=1}^{n-1}\frac{1}{(1-z^k)^2}$ - the sum whose value we are to specify. On the right, $\displaystyle f(1)=\sum_{k=1}^{n-1}k=\frac{(n-1)n}{2};$ $\displaystyle g(1)=\sum_{k=0}^{n-1}1=n;$ $\displaystyle g'(1)=f(1)=\frac{(n-1)n}{2};$ $\displaystyle f'(1)=\sum_{k=2}^{n-1}k(k-1)=\frac{(n-1)n(2n-1)}{6}-\frac{(n-1)n}{2}.$ So we can continue

$\displaystyle\begin{align}\sum_{k=1}^{n-1}\frac{1}{(1-z^k)^2}&=-\frac{f'g-fg'}{g^2}\\ &=-\frac{\displaystyle \left(\frac{(n-1)n(2n-1)}{6}-\frac{(n-1)n}{2}\right)\cdot n-\frac{(n-1)n}{2}\cdot\frac{(n-1)n}{2}}{n^2}\\ &=-(n-1)\frac{4n-2-6-3n+3}{12}=-\frac{(n-1)(n-5)}{12}. \end{align}$

Let $\displaystyle f(Z)=\sum_{k=0}^{n-1}Z^k.$

$\displaystyle \begin{align} \sum_{k=1}^{n-1}\frac{1}{(1-z^k)^2}&=\left(\sum_{k=1}^{n-1}\frac{1}{1-z^k}\right)^2-2\sum_{1\le t\lt s\le n-1}\frac{1}{(1-z^t)(1-z^s)}\\ &=\frac{(n-1)^2}{4}-\frac{f''(1)}{f(1)}=\frac{(n-1)^2}{4}-\frac{(n-1)(n-2)}{3}\\ &=-\,\frac{(n-1)(n-5)}{12}. \end{align}$

With a reference to the diagram below, $\displaystyle\arg\left(\frac{1-z}{|1-z|}\right)=- \frac{1}{2}(\pi-\alpha).$

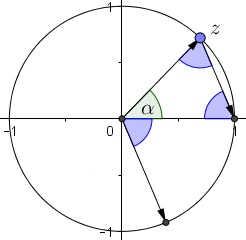
For $\displaystyle \alpha=\frac{2\pi}{n},$ this gives $\displaystyle -\frac{2\pi(n-2)}{4n}.$ If we denote $\displaystyle w=\frac{1-z}{|1-z|},$ then $w^{4n}=e^{-2\pi(n-2)i}=1.$

Let, as before, $\displaystyle z = \exp\left(\frac{2\pi i}{n}\right),$ and

$\displaystyle f(Z)=\frac{Z^n-1}{Z-1}=\sum_{k=0}^{n-1}Z^k.$

The roots of the equation $f(Z)=0$ are all the distinct $n^{th}$ roots of unity with the exception of unity itself. Thus,

$\displaystyle f(Z) =\prod_{k=1}^{n-1}(Z-z^k).$

Plugging in $Z=1$ in the expression for $f(Z)$,

$\displaystyle f(1)=\prod_{k=1}^{n-1}(1-z^k)=\sum_{k=0}^{n-1}1^k=n.$

Further,

$\displaystyle \begin{align} \sum_{k=1}^{n-1}\frac{1}{(Z-z^k)}&=\frac{1}{f(Z)}\frac{df(Z)}{dZ}=\frac{ \sum_{k=0}^{n-1} kZ^{k-1}}{\sum_{k=0}^{n-1} Z^k}, \\ -\sum_{k=1}^{n-1}\frac{1}{(Z-z^k)^2}&=\frac{d}{dZ}\left[\frac{1}{f(Z)}\frac{df(Z)}{dZ}\right] \\ &=\frac{\left(\sum_{k=0}^{n-1} Z^k\right) \left(\sum_{k=0}^{n-1}k(k-1)Z^{k-2}\right) -\left(\sum_{k=0}^{n-1} kZ^{k-1}\right)^2}{\left(\sum_{k=0}^{n-1} Z^k\right)^2} \end{align}$

Plugging in $Z=1$,

$\displaystyle \begin{align}\sum_{k=1}^{n-1}\frac{1}{(1-z^k)}&=\frac{\sum_{k=1}^{n-1}k}{\sum_{k=1}^{n-1}} =\frac{n(n-1)}{2}\cdot\frac{1}{n}=\frac{n-1}{2}, \\ -\sum_{k=1}^{n-1}\frac{1}{(1-z^k)^2}&=\frac{n \left(\sum_{k=0}^{n-1}k(k-1)\right)-\left(\frac{n(n-1)}{2}\right)^2}{n^2} \\ &=\frac{n \left(\frac{n(n-1)(2n-1)}{6}-\frac{n(n-1)}{2}\right)-\left(\frac{n(n-1)}{2}\right)^2}{n^2} \\ &=\frac{(n-1)}{2}\left[\frac{2n-1}{3}-1-\frac{n-1}{2}\right]=\frac{(n-1)(n-5)}{12}. \end{align}$

The four questions above have been posted at different times by Samuel Walters on twitter.com. Abdallah El Farissi came up with solutions to the first two questions; Leo Giugiuc added solutions to the first three. N. N. Taleb made use of power tools for a solution to question 1 and also to solve question 2. The unified solution is by Amit Itagi.