An Equation in $\mathbb{R^2}$ from Romania
Problem
Solution 1
With the substitution $a=x-2,\,$ $b=y+3,$ the equation becomes
$(a^2+a+1)(b^2-b+1)=3ab.$
There clearly no solutions when $ab\le 0.$
Case 1: $\mathbf{a,b\gt 0}$
Rewrite the equation as $\displaystyle \left(a+\frac{1}{a}+1\right)\left(b+\frac{1}{b}-1\right)=3\,$ and set $\displaystyle a+\frac{1}{a}=u+2\,$ and $\displaystyle b+\frac{1}{b}=v+2.$ Obviously, $u,v\ge 0.$ The equation reduces to $uv+u+3v=0,\,$ yielding $u=v=0,\,$ i.e., $a=b=1,\,$ or $x=3,\,$ $y=-2.$
Case 2: $\mathbf{a,b\lt 0}$
Similar to the previous case, we obtain $a=b=-1,\,$ i.e., $x=1\,$ and $y=-4.$
Solution 2
For the equation
$\displaystyle (x^2-3x+3)(y^2+5y+7)=3(x-2)(y+3)$
we can factorize as
$\displaystyle [(x-2)(x-1)+1][(y+3)(y+2)+1]=3(x-2)(y+3)$
Let $u=x-2$ and $v=y+3$. The above equation becomes:
$\displaystyle [u(u+1)+1][v(v-1)+1]=3uv$
Separating the variables:
$\displaystyle \frac{u(u+1)+1}{u}=\frac{3v}{v(v-1)+1}$
which can be expressed as
$\displaystyle u+\frac{1}{u}+1=\frac{3}{v+\frac{1}{v}-1}$
First we observe that $u$ and $v$ must have same signs.
For $u,v\gt 0$, $\displaystyle u+\frac{1}{u}\geq2$ and $\displaystyle v+\frac{1}{v}\geq 2$. So, the $LHS\geq3$ while $RHS\leq3$. Thus, the equality happens only if $LHS=RHS=3$ which would be true for $u=v=1$ leading to $(x_1,y_1)=(3,-2)$.
For $u,v\lt 0$, $\displaystyle u+\frac{1}{u}\leq-2$ and $\displaystyle v+\frac{1}{v}\leq -2$. So, the $LHS\leq-1$ while $RHS\geq-1$. Thus, the equality happens only if $LHS=RHS=-1$ which would be true for $u=v=-1$ leading to $(x_2,y_2)=(1,-4)$.
Solution 3
Note that $x^2-3s+3\gt 0$ for all $x\in\mathbb{R}$ whereas $y^2+5y+7\gt 0$ for all $y\in\mathbb{R}.$ In particular, $x=2\,$ could not be a part of any solution. Consider two functions:
$\displaystyle \begin{align} f(x)&=\frac{x^2-3x+3}{x-2}\\ g(y)&=\frac{3(y+3)}{y^2+5y+7}. \end{align}$
Below are their graphs:
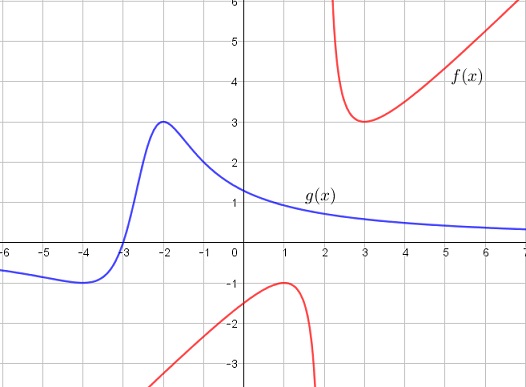
Note that $Im(f)=(-\infty,1]\cup [3,\infty)\,$ whereas $Im(g)=[-1,3].$ It follows that $f(x)=g(y)$ is possible if $(x,y)=(1,-4)$ or $(x,y)=(3,-2).$
Solution 4
Note that $x^2-3s+3\gt 0$ for all $x\in\mathbb{R}$ whereas $y^2+5y+7\gt 0$ for all $y\in\mathbb{R}.$
For all $x\in\mathbb{R},$ $x^2-3x+3\ge 3x-6\,$ with equality at $x=3$ because $x^2-3x+3- 3x+6=(x-3)^2.$
For all $y\in\mathbb{R},$ $y^2+5y+7\ge y+3\,$ with equality at $y=-2$ because $y^2+5y+7-y-3=(y+2)^2.$

It follows that $(x^2-3x+3)(y^2+5y+7)\gt (3x-6)(y+3)$ unless $x=3$ and $y=-2.$
On the other hand,
For all $x\in\mathbb{R},$ $x^2-3x+3\ge 2-x\,$ with equality at $x=1$ because $x^2-3x+3-2+x=(x-1)^2.$
For all $y\in\mathbb{R},$ $y^2+5y+7\ge -3(y+3)\,$ with equality at $y=-4$ because $y^2+5y+7+3(y+3)=(y+4)^2.$
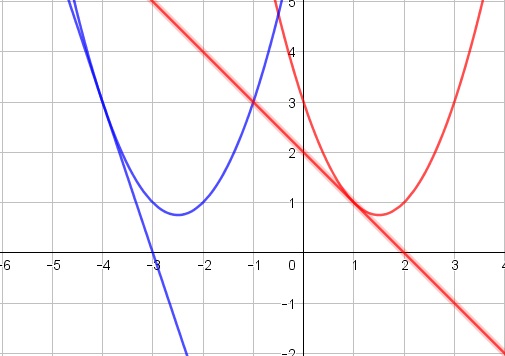
It follows that $(x^2-3x+3)(y^2+5y+7)\gt -(2-x)3(y+3)$ unless $x=1$ and $y=-4.$
Solution 5
Let,
$\frac{x^2-3x+3}{x-2}=\frac{3(y+3)}{y^2+5y+7}=k.$
Thus,
$\displaystyle \begin{align} &x^2-(3+k)x+(2k+3)=0 \\ &y^2+\left(5-\frac{3}{k}\right)y+\left(7-\frac{9}{k}\right)=0. \end{align}$
For real roots, the discriminants of the two equations have to be non-negative. Thus,
$\displaystyle \begin{align} &(3+k)^2-4(2k+3)\geq 0 \\ &\left(5-\frac{3}{k}\right)^2-4\left(7-\frac{9}{k}\right)\geq 0. \end{align}$
The two inequalities simplify to $k^2-2k\geq 3$ and $3\geq k^2-2k$. Thus, the only possibility is that the inequalities becomes an equality, $k^2-2k=3$, the discriminants become $0$ and we get coincident roots for the quadratic equations in $x$ and $y$. Thus $k=3$ or $k=-1$;
$\displaystyle \begin{align} &x^2-6x+9=0 \\ &y^2+4x+4=0, \end{align}$
or
$\displaystyle \begin{align} &x^2-2x+1=0 \\ &y^2+8x+16=0. \end{align}$
Thus, $(x,y)=(3,-2)$ or $(x,y)=(1,-4)$.
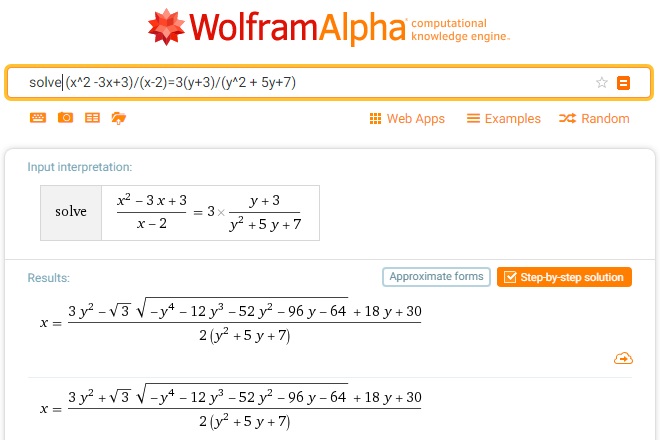
From wolframalpha 1
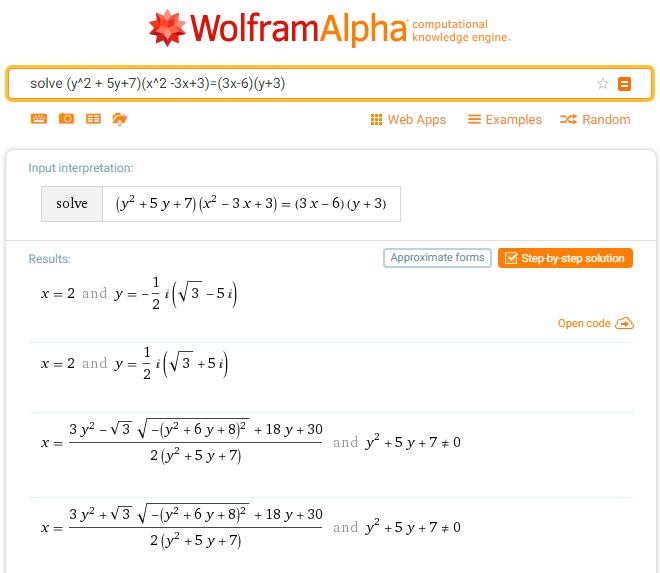
From wolframalpha 2
Acknowledgment
The problem has been posted by Leo Giugiuc on the online Community of Romanian Mathematics Teachers (Comunitatea profesorilor de matematică din România). The problem is by Stelian Corneliu Andronescu and Costel Bălcău. Solution 1 is by Leo Giugiuc; Solution 2 is by Faryad D. Sahneh; Solution 3 is by Claudia Tanase; Solution 4 is by Lorenzo Villa; Solution 5 is by Amit Itagi. Jonathan D. Evenboer came up with the idea of employing wolframalpha. As can be seen from above, two attempts proved fruitless.
![]()
|Contact| |Up| |Front page| |Contents| |Arithmetic|
Copyright © 1996-2018 Alexander Bogomolny73573414
