Another Property of Number 4

This is a follow-up on an earlier problem posed by Dorin Marghidanu:

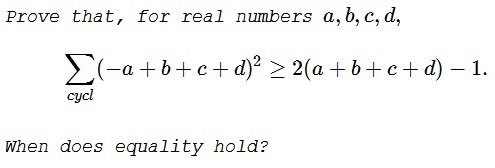
All solutions to the latter problem used - in one way or another - the fact that

$\displaystyle \sum_{cycl}(-a+b+c+d)^2=4\sum_{cycl}a^2.$

Hence the question:

This is not possible for $n=3.\,$ For $n=4,\,$ $\alpha=(-1,1,1,1)\,$ and permutations. We hope prove that $n=4\,$ serves a unique answer to our question which explains the caption of the page.

The sections below have been added successively, following the announcements of the results.

1. Amit Itagi has shown that in case where there are exactly two contiguous groups of signs, $4\,$ is the only possible answer to the posted question.

2. The twitter user Long has remarked that Amit's argument could not be extended to the case of non-contiguous groups.

3. Tim Robinson has observed that any solution to the posted problem ought to be a multiple of $4.$

4. It was not difficult to show that the number $n\,$ needs to be a square.

The solution is by Amit Itagi.

In what follows we shall refer to $\displaystyle \sum_{cycl}\left((\alpha_1,\alpha_2,\alpha_3,\ldots)\cdot (a,b,c,\ldots)\right)^2=n\sum_{cycl}a^2\,$ as Condition I.

For some $n$, let us denote one of the cyclic terms by $\sigma_1 a_1+\sigma_2 a_2+...+\sigma_n a_n$ where $a_i\text{'s}$ are the variables and $\sigma_i\in\{+1,-1\}$. We also assume that in the first term, the first $k$ $\sigma_i\text{'s}$ are $+1$ and the remaining $n-k$ $\sigma_i\text{'s}$ are $-1$. Now, construct a matrix by cyclically permuting each row by one step starting from the first row.

$\begin{align} \begin{bmatrix} \sigma_1 & \sigma_2 & \dots & \sigma_{n-1} & \sigma_n \\ \sigma_2 & \sigma_3 & \dots & \sigma_n & \sigma_1 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \sigma_n & \sigma_1 & \dots & \sigma_{n-2} & \sigma_{n-1} \end{bmatrix} \end{align}$

This is a symmetric matrix and the coefficient of $a_ia_j$ $(i\ne j)\,$ term in the LHS of the Condition I is just twice the dot product of the $i^{th}$ and the $j^{th}$ column of this matrix. The dot product of any column with itself is $n$.

Let us assume that there exists a solution for $n\gt 4$. From our assumption, the dot product of the first and second column has to be $0$ (condition I). There cannot be any non-zero cross-terms on the RHS.

Case 1: Let all $\sigma_i\text{'s}$ be equal. In that case, the dot product of the first two columns will also be $n$ and our assumption is being contradicted.

Case 2: $k\in\{2,...,n-1\}$ i.e we have some terms $+1$ and some $-1$. In this case, if $C_i$ represents the $i^{th}$ column, the column transposes are given by

$\begin{align} C_1^t&=[(+1)_{k~terms}~(-1)_{n-k~terms}] \\ C_2^t&=[(+1)_{k-1~terms}~(-1)_{n-k~terms}~(+1)_{1~term}] \end{align}$

Note, the only difference between $C_1\cdot C_1$ and $C_1 \cdot C_2$ is that the $k^{th}$ and the $n^{th}$ terms have switched from $+1$ to $-1$ in the dot product. Thus,

$C_1\cdot C_2 = C_1\cdot C_1 - 4 = n-4.$

Thus, from condition I, $n-4=0$. This is not possible for $n\gt 4$ and our assumption is contradicted. Hence, no solutions are possible for $n\gt 4$.

The below is similar to the matching argument in the problem of two colors in two rows.

Let there be $m\,$ minuses in a row of $n\,$ numbers. Compare this row $X\,$ with some non-trivial rotation of it $Y.\,$ Let $p\,$ minuses in $X\,$ match up with minuses in $Y.\,$ Then $m-p\,$ minuses in $X\,$ match up with pluses in $Y,\,$ and $m-p\,$ minuses in $Y\,$ match up with pluses in $X.\,$ So the total number of minus products is $2\cdot (m-p),\,$ and this must be added to an equal number of plus products to come out at zero. So the total number of products $n\,$ is $4\cdot (m-p).\,$ So $n=4(m-p)\,$ and is divisible by four.

Remark: one direction to look into that seems promising is that, for fixed $n\,$ and $m,\,$ $p\,$ needs to be constant, indpendent of the rotation of a sequence of signs.

It is convenient to number the variables, say, $x_1,x_2,\ldots,x_n,x_{n+1}=x_1,\,$ etc. Similarly, $\alpha_{n+1}=\alpha_1,\,$ etc. Then

$\displaystyle\begin{align} \sum_{cycl}\left((\alpha_1,\alpha_2,\alpha_3,\ldots)\cdot (a,b,c,\ldots)\right)^2&=\sum_{t=0}^{n-1}\left(\sum_{k=1}^n\alpha_kx_{k+t}\right)^2\\ &=\sum_{t=0}^{n-1}\left(\sum_{k,m=1}^n\alpha_k\alpha_mx_{k+t}x_{m+t}\right)\\ &=\sum_{k,m=1}^n\sum_{t=0}^{n-1}\alpha_{k-t}\alpha_{m-t}x_{k}x_{m}\\ &=\sum_{k,m=1}^nx_{k}x_{m}\left(\sum_{t=0}^{n-1}\alpha_{k-t}\alpha_{m-t}\right)\\ &=\sum_{k,m=1}^nx_{k}x_{m}\left(\sum_{s=0}^{n-1}\alpha_{k+s}\alpha_{m+s}\right)\\ \end{align}$

Obviously, $\displaystyle \sum_{s=0}^{n-1}\alpha_{k+s}\alpha_{k+s}=n,\,$ for all $k.\,$ The question then reduces to whether or not $\displaystyle \sum_{s=0}^{n-1}\alpha_{k+s}\alpha_{m+s}=0,\,$ for all $k,m,k\ne m.\,$ In other words, whether or not $\displaystyle \sum_{p=1}^{n}\alpha_{p}\alpha_{p+\delta}=0,\,$ for all $\delta=1,2,\ldots,n-1.\,$ Assume this is so. Then, setting $\displaystyle s=\sum_{q=1}^{n}\alpha_q,\,$ we have

$\displaystyle\begin{align} 0&=\sum_{\delta=1}^{n-1}\left(\sum_{p=1}^{n}\alpha_{p}\alpha_{p+\delta}\right)=\sum_{p=1}^{n}\alpha_p\left(\sum_{\delta=1}^{n-1}\alpha_{p+\delta}\right)\\ &=\sum_{p=1}^{n}\alpha_p\left(\sum_{q=1}^{n}\alpha_{q}-\alpha_{p}\right)\\ &=\sum_{p=1}^{n}\alpha_p\left(s-\alpha_{p}\right)\\ &=s^2-\sum_{p=1}^n\alpha_{p}^2=s^2-n. \end{align}$

Thus $n=s^2.\,$