Two Solutions: One Correct, One Illuminating. An Example
Problem
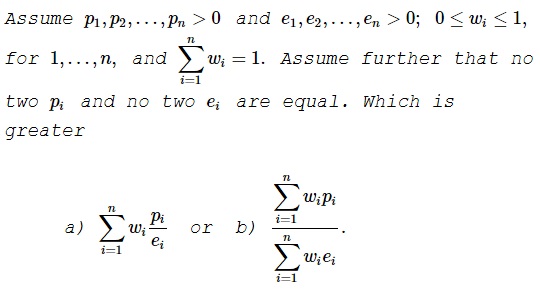
Solution 1
Which of the two quantities is greater depends on specific values of the variables. We show that by two examples. In both examples we'll have $n=2\,$ and $w_1=w_2=\displaystyle\frac{1}{2}.$
Example 1: $p_1=1,p_2=4,e_1=1,e_2=2.$
$\displaystyle a=\frac{1}{2}(1+2)=\frac{3}{2},\,b=\frac{\displaystyle\frac{1}{2}(1+4)}{\displaystyle\frac{1}{2}(1+2)}=\frac{5}{3}\,\Rightarrow\, a\lt b.$
Example 2: $p_1=1,p_2=2,e_1=1,e_2=4.$
$\displaystyle a=\frac{1}{2}(1+\frac{1}{2})=\frac{3}{4},\,b=\frac{\displaystyle\frac{1}{2}(1+2)}{\displaystyle\frac{1}{2}(1+4)}=\frac{3}{5}\,\Rightarrow\, a\gt b.$
Solution 2
Let $X,Y$ be random variables and $A_1,...,A_n$ be events with
* $P(A_i) = \omega_i$
* $\{X = e_i \} = A_i = \{ Y = p_i/e_i\}$
for all $i$. Plugging this into the formula for the covariance
$\displaystyle Cov(X,Y) = E(XY)-E(X)E(Y) $
we obtain
$\displaystyle Cov(X,Y) = \sum_i \omega_i p_i - \sum_i \omega_i e_i \sum_i \omega_i \frac{p_i}{e_i}. $
The inequality now depends on whether $Cov(X,Y)$ is positive or negative; either of which may be the case.
Remark
The difference in the usefulness of the two solutions is noteworthy. The first one answers the question posed, but does not add to our understanding of the question or of the answer.
The second solution not only answers the question but also removes the mystery left over by the first solution. In general terms, the covariance is positive if the values of the two variables are aligned (something akin to the Rearrangement or Chebyshev's inequalities), i.e., greater values of one correspond to greater values of the other. The covariance is negative if the alignment is reversed. This is clearly confirmed by the examples in Solution 1 with the choice of the random variables from Solution 2.
Acknowledgment
The problem has been twitted by N. N. Taleb. Solution 2 is by Long Huynh Huu.
N. N. Taleb remarks that the notations in the problem have real life context: $p_i$ is the price of company $i,\,$ $e_i\,$ is earnings, $w_i\,$ is the percentage of the market capitalization. Both $a\,$ and $b\,$ express the price to earnings ratio. The first is the weighted average of the P/E of indivisual companies; the second is that of the market.
![]()
|Contact| |Front page| |Contents| |Algebra| |Probability|
Copyright © 1996-2018 Alexander Bogomolny73573607
