A Limit With Sums, Roots, And Binomial Coefficients
Problem
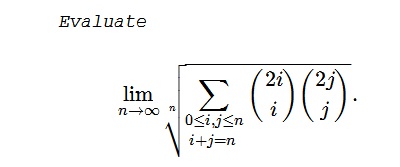
Solution 1
$\displaystyle \sum_{k=0}^n(1+x)^{2k}(1+x)^{2n-2k}=(n+1)(1+x)^{2n}.$ Comparing the coefficients of $x^n$ on both sides,
$\displaystyle \sum_{0\le i,j\le n\\\,i+j=n}{2i\choose i}{2j\choose j}=(n+1){2n\choose n}.$
To continue,
$\displaystyle\begin{align}\lim_{n\to\infty}\sqrt[n]{\sum_{0\le i,j\le n\\\,i+j=n}{2i\choose i}{2j\choose j}}&=\lim_{n\to\infty}\sqrt[n]{(n+1){2n\choose n}}\\ &=\lim_{n\to\infty}\frac{n+2}{n+1}\cdot\frac{\displaystyle \frac{(2n+2)!}{((n+1)!)^2}}{\displaystyle \displaystyle\frac{(2n)!}{(n!)^2}}\\ &=\lim_{n\to\infty}\frac{(n+2)(2n+2)(2n+1)}{(n+1)(n+1)^2}=4. \end{align}$
Solution 2
The generating function fir the central binomial coefficient is $(1-4x)^{-\frac{1}{2}},$ that is
$\displaystyle \sum_{i=0}^{\infty}{2i\choose i}x^i=\frac{1}{\sqrt{4x-1}}.$
It follows that
$\displaystyle \sum_{0\le i,j\le n\\\,i+j=n}{2i\choose i}{2j\choose j}=\sum_{i=0}^n{2i\choose i}{2(n-i)\choose n-i}$
is the coefficient of $x^n$ in the function
$\displaystyle \frac{1}{\sqrt{4x-1}}\cdot\frac{1}{\sqrt{4x-1}}=\frac{1}{4x-1}=\sum_{n=0}^{\infty}(4x)^n,$
which is $4^n.$ Thus
$\displaystyle\lim_{n\to\infty}\sqrt[n]{\sum_{0\le i,j\le n\\\,i+j=n}{2i\choose i}{2j\choose j}}=\lim_{n\to\infty}\sqrt[n]{4^n}=4.$
Solution 3
It's well known that for $\displaystyle |x|\le\frac{1}{4},$ $\displaystyle \sum_{i=0}^{\infty}{2i\choose i}x^i=\frac{1}{\sqrt{4x-1}},$ with the usual convention that $0!=1$ and $\displaystyle {0\choose 0}=1.$ Hence,
$\displaystyle \begin{align} \sum_{i=0}^{\infty}(4x)^i&=\frac{1}{4x-1}=\left(\sum_{i=0}^{\infty}{2i\choose i}x^i\right)^2\\ &=\sum_{n=0}^{\infty}\sum_{0\le i,j\le n\\\,i+j=n}{2i\choose i}{2j\choose j}x^n. \end{align}$
Thus for nonnegative integers $n,$
$\displaystyle \sum_{0\le i,j\le n\\\,i+j=n}{2i\choose i}{2j\choose j}=4^n,$
so that the limit at hand equals $4.$
Solution 4
First off, $\displaystyle {2j\choose j}{2(n-j)\choose n-j}\le{2n\choose n},$ for $0\le j\le n$ which can be proved by induction on $n.$ From here,
$\displaystyle {2n\choose n}\le\sum_{j=0}^n{2j\choose j}{2(n-j)\choose n-j}\le (n+1){2n\choose n}.$
Taking the $n^{th}$ root and using the fact that $\displaystyle \lim_{n\to\infty}(n+1)^{\frac{1}{n}}=1,$
$\displaystyle \lim_{n\to\infty}\sqrt[n]{\sum_{j=0}^n{2j\choose j}{2(n-j)\choose n-j}}=\lim_{n\to\infty}\sqrt[n]{{2n\choose n}}.$
Now, with the Sterling formula, $\displaystyle n!\asymp\sqrt{2\pi n}\left(\frac{n}{e}\right)^n,$ it is obvious that $\displaystyle \lim_{n\to\infty}\sqrt[n]{{2n\choose n}}=4.$
Solution 5
We have $\displaystyle \binom{2 a}{a}=\frac{2^{2 a} \Gamma \left(a+\frac{1}{2}\right)}{\sqrt{\pi } \Gamma (a+1)}.$ Hence
$\displaystyle \binom{2 i}{i} \binom{2 (n-i)}{n-i}=\frac{2^{2 n} \Gamma \left(i+\frac{1}{2}\right) \Gamma \left(-i+n+\frac{1}{2}\right)}{\pi \Gamma (i+1) \Gamma (-i+n+1)}$
Summing up
$\displaystyle \begin{align} \sum _{i=0}^n \frac{4^n \Gamma \left(i+\frac{1}{2}\right) \Gamma \left(-i+n+\frac{1}{2}\right)}{\pi \Gamma (i+1) \Gamma (-i+n+1)}&=\frac{4^n \Gamma \left(n+\frac{1}{2}\right)}{\sqrt{\pi } \Gamma (n+1)}+\frac{2^{2 n-1} \Gamma \left(n-\frac{1}{2}\right)}{\sqrt{\pi } \Gamma (n)}\\ &+\frac{3\ 2^{2 n-3}\Gamma \left(n-\frac{3}{2}\right)}{\sqrt{\pi } \Gamma (n-1)}+\frac{5\ 4^{n-2} \Gamma \left(n-\frac{5}{2}\right)}{\sqrt{\pi } \Gamma (n-2)}\\ &+\frac{35\ 2^{2 n-7} \Gamma\left(n-\frac{7}{2}\right)}{\sqrt{\pi } \Gamma (n-3)}+\frac{63\ 4^{n-4} \Gamma \left(n-\frac{9}{2}\right)}{\sqrt{\pi } \Gamma (n-4)} \end{align}$
Hence
$\displaystyle \lim_{n\to \infty}\left(2^{2 n} \sum _{i=0}^n \frac{\Gamma \left(i+\frac{1}{2}\right) \Gamma \left(-i+n+\frac{1}{2}\right)}{\pi \Gamma (i+1) \Gamma (-i+n+1)}\right)^{1/n}=4$
Acknowledgment
This problem 5448 from the SSMA magazine. The problem has been proposed by Yubal Barrios and Ángel Plaza (Spain). I am greatful to Dan Sitaru (Romania) for communicating to me one of his solutions (Solution 1), along with several published ones. Solution 2 is by Brian Bradie (USA); Solution 3 is be Kee-Way Lau (Hong-Kong); Solution 4 is by Sam Walters; Solution 5 is by N. N. Taleb.
![]()
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73518315
