Check for Negative Roots
Problem
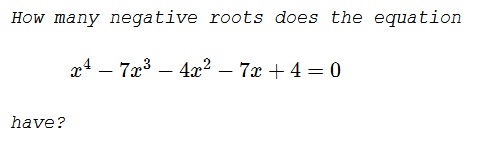
Solution 1
$x^4-7x^3-4x^2-7x+4=(x^2-2)^2-7x(x^2+1)\gt 0$ for all $x\lt 0.$ There are no negative roots.
Solution 2
$x^4-7x^3-4x^2-7x+4=(x^2 + x - 2)^2 - x\cdot (9x^2 + x + 3)$ and $9x^2 + x + 3\ge 0$ for all $x.$
Solution 3
Plug in $y=-x.$ $y^4+7y^3-4y^2+7y+4=(y^2-2)^2+7y(y^2+1)\gt 0$ for $y\gt 0.$ Thus, no negative roots.
Solution 4
$0.$ With $x$ replaced by $-x,$ $f(x)=x^4+7x^3-4x^2+7x+4.$ If $x\ge 1,$ $7x^3\gt 4x^2.$ If $0\le x\lt 1,$ $4\gt 4x^2$ and the rest of the terms are non-negative.
Solution 5
None. If there were, then $4x^2 = x^4-7x^3-7x+4\ge 4$ and so $x\le -1.$ But then $-7x^3\gt -4x^2,$ making $x^4-7x^3-4x^2-7x+4 \gt 0.$
Solution 6
None, because
$\displaystyle x^4-7x^3-4x^2-7x+4=x^4+4-7x\left(\left(x+\frac{2}{7}\right)^2+\frac{45}{49}\right) \gt 0,$
while $x^4+4\gt 0$ and $\displaystyle \left(x+\frac{2}{7}\right)^2+\frac{45}{49}\gt 0$ for all $x$ which means that $x^4-7x^3-4x^2-7x+4\gt 0$ for $x\lt 0.$
Solution 7
Note $-1$ is not a root and we recover the original polynomial with the substitution $\displaystyle x \rightarrow \frac{1}{x}.$ Thus, if we can show the roots $\gt -1$ we have shown there are no negative roots. But $P(-x-1)$ has all positive coefficients, hence $-x-1 \lt 0,$ implying $x \gt -1.$
Solution 8
The derivative could be written as
$4x^3-21x^2-8x-7=4x^3 -17x^2 - 4(x+1)^2 - 3\lt 0,$
since each term is negative for $x\lt 0,$ hence, $f(x)\ge f(0)=4.$
Acknowledgment
This is a slight modification of problem 8 from Charles W. Trigg's Mathematical Quickies (Dover, 1985). The problem, with a solution, was previously published in the Mathematics Magazine 24 (November, 1950, p 114) by R. E. Horton.
Solution 2 is by Mike Lawler; Solution 3 is by Amit Itagi; Solution 4 is by Bogdan Lataianu; Solution 5 is by Kevin Knudson; Solution 6 is by Gary Davis; Solution 7 ia by Christopher D. Long; Solution 8 is by Fredrik Andréasson. Deepak Venkatesh and Harshal Bhadkamkar have independently come with Solution 1.
![]()
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73580199
