A Limit of a Series of Determinants
Problem
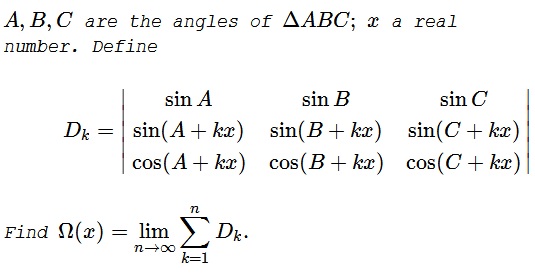
Solution 1
We apply row operations to the determinant:
$\begin{align} D_k&=\left|\begin{array}{ccc} \sin A & \sin B & \sin C\\\sin(A+kx) & \sin(B+kx) & \sin(C+kx)\\\cos(A+kx) & \cos(B+kx) & \cos(C+kx)\end{array}\right|^{r_2=r_2-(\cos(kx))r_1\\r_3=r_3-(\sin (kx))r_1}\\\\ &=\left|\begin{array}{ccc} \sin A & \sin B & \sin C\\\cos(A)\sin(kx) & \cos (B)\sin(kx) & \cos(C)\sin(kx)\\\cos(A)\cos(kx) & \cos(B)\cos(kx) & \cos(C)\cos(kx)\end{array}\right|\\\\ &=0, \end{align}$
since rows $r_2$ and $r_3$ are linearly dependent:
$(\cos(kx))r_2-(\sin(kx))r_3=0.$
The sought limit is therefore $0.$
Solution 2
Let's remark that $D_k$ is real. Multiply the second row by $i$ and add that to the third row to obtain
$D_k=(\cos(xk)+i\sin (xk))\left|\begin{array}{ccc} \sin A & \sin B & \sin C\\\sin(A+kx) & \sin(B+kx) & \sin(C+kx)\\\cos(A) & \cos(B) & \cos(C)\end{array}\right|.$
If $\sin(kx)\ne 0,$ then, since $D_k$ is real,
$\left|\begin{array}{ccc} \sin A & \sin B & \sin C\\\sin(A+kx) & \sin(B+kx) & \sin(C+kx)\\\cos(A) & \cos(B) & \cos(C)\end{array}\right|=0.$
Hence, $D_k=0.$ If $\sin(xk)=0,$ then $kx=m\pi,$ implying the linear dependence of the first two rows. So, $D_k=0,$ in this case as well.
Solution 3
For all $k$,
$\displaystyle \begin{align} D_k&=\sum_{cyc} \sin A[\sin (B+kx) \cos (C+kx)-\cos (B+kx) \sin (C+kx)] \\ &=\sum_{cyc}\sin A \sin(B-C) =\sum_{cyc}\sin (B+C) \sin(B-C) \\ &=\sum_{cyc}\frac{1}{2}(\cos 2C - \cos 2B)=0. \end{align}$
Thus, the limit is $0$.
Acknowledgment
The problem, with a solution, was kindly posted at the CutTheKnotMath facebook page by Dan Sitaru. The problem is by Dan and was previously published in the Romanian Mathematical Magazine. Solution 1 is by Ravi Prakash, Solution 2 is by Leo Giugiuc; Solution 3 is by Amit Itagi.
It may be observed that the requirement that $A,B,C$ be the three angles of a triangle is a red herring.
![]()
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73579330
