Functional Inequality from Vietnam
Problem
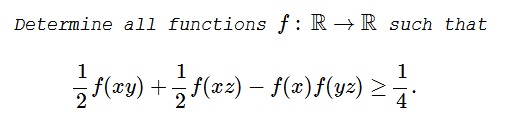
Solution
Setting $x=y=z=0$ one gets
$\frac{1}{2}f(0)+\frac{1}{2}f(0)-f^2(0)\ge\frac{1}{4}$
which is equivalent to $\displaystyle \left(f(0)-\frac{1}{2}\right)^2\le 0,$ so that $\displaystyle f(0)=\frac{1}{2}.$ Similarly, $\displaystyle f(1)=\frac{1}{2}.$
Now setting $y=z=0,$
$\displaystyle \frac{1}{2}f(0)+\frac{1}{2}f(0)-f(x)f(0)\ge\frac{1}{4}$
so that $\displaystyle f(x)\le\frac{1}{2}.$ Setting $y=z=1,$
$\displaystyle \frac{1}{2}f(x)+\frac{1}{2}f(x)-f(x)f(1)\ge\frac{1}{4}$
results in $\displaystyle f(x)\ge\frac{1}{2}.$ Thus $\displaystyle f(x)=\frac{1}{2},$ for all $x\in\mathbb{R}.$
Acknowledgment
This problem is from the Vietnamese National Olympiad in Mathematics for Secondary Schools, 1991. It was published in the Canadian Crux Mathematicorum (December 1992), with the solution in a later issue.
![]()
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73580509
