Fixed Point of a Family of Parabolas
What Is This About?
Problem
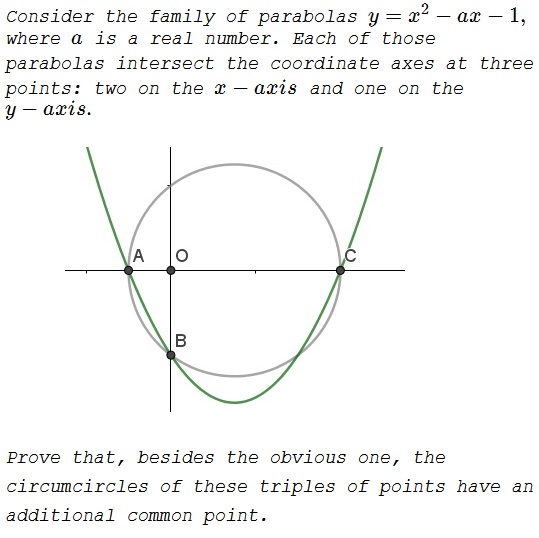
Solution 1
Every equation $x^2-ax-1=0$ has two real solutions, say, $x_1$ and $x_2$ that satisfy $x_1x_2=-1.$ For definiteness' sake, assume $x_1\lt 0\lt x_2,$ so that the parabola $y=x^2-ax-1$ intersects the $x-axis$ at two points $A=(x_1,0)$ and $C=(x_2,0).$ Also, the parabola intersects the $y-axis$ at $B=(0,-1).$ Let $D=(0,d)$ be the second point of intersection of the circumcircle
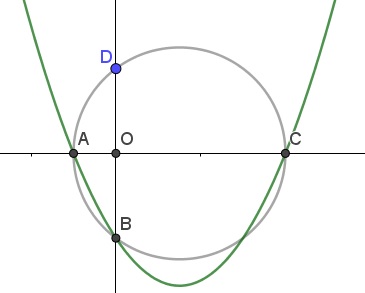
Let $O$ denote the origin. Then, by the intersecting chords theorem, $AO\cdot CO=BO\cdot DO,$ or $1=|x_1|\cdot x_2=|-1|\cdot d,$ implying $d=1.$ It follows that all the circumcircles pass through $D=(0,1).$
Solution 2
The three common points obtained from $y=x^2-ax-1|_{x=0}$ and $y=x^2-ax-1|_{y=0}$ are
$\displaystyle A=\left(\frac{a+\sqrt{a^2+4}}{2},0\right),~ B=\left(\frac{a-\sqrt{a^2+4}}{2},0\right),~ C=(0,-1).$
The center of the circle - $O$ - lies on the perpendicular bisector of $AB$. Thus, the coordinates of the center are of the form $(a/2,h)$ for some real $h$. Plugging in the coordinates of $A$ and $C$ in the equation of the circle $(x-x_c)^2+(y-y_c)^2=r^2$ and eliminating the radius $r$, the following equation if obtained:
$\displaystyle \frac{a^2}{4}+(h+1)^2=\frac{a^2+4}{4}+h^2.$
Solving the equation, we get $h=0$. Thus, the center of the circle is $(a/2,0)$, $AB$ is a diameter, and by symmetry, the other common point of the family of circles is the reflection of $(0,-1)$ about the $X$ axis - the point $(0,1)$.
Acknowledgment
Solution 2 is by Amit Itagi.
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny
73572908
