An Equation in Factorials
Problem
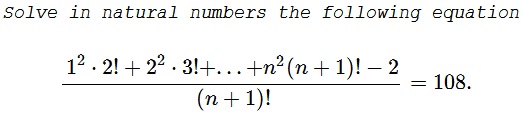
Solution 1
We'll use the induction in $n\,$ to prove
$1^2\cdot 2!+2^2\cdot 3!+\ldots+n^2(n+1)!-2=(n+2)!(n-1).$
The claimholds for $n=1:\,$ $1^2(1+1)!-2=(1+1)(1+2)(1-1).$
Assume $P(k)=:\,1^2\cdot 2!+2^2\cdot 3!+...+k^2(k+1)!-2=(k+2)!(k-1)\,$ is true, and let's prove $P(k+1),\,$ i.e.,
$1^2\cdot 2!+2^2\cdot 3!+...+k^2(k+1)!+(k+1)^2(k+2)!-2=(k+3)!k.$
We have
$\begin{align} &1^2\cdot 2!+2^2\cdot 3!+...+k^2(k+1)!+(k+1)^2(k+2)!-2\\ &\qquad\qquad\qquad=(k+2)!(k-1)+(k+1)^2(k+2)!\\ &\qquad\qquad\qquad=(k+2)![(k-1)+(k+1)^2]\\ &\qquad\qquad\qquad=(k+2)![k^2+3k]\\ &\qquad\qquad\qquad=(k+3)!k, \end{align}$
as required. Thus we rewrite the original equation:
$\displaystyle \frac{(n+2)!(n-1)}{(n+1)!}=108,$
or, $n^2+n-110=0,\,$ giving two roots, $n=10\,$ that solves the problem and a superfleous one $n=-11.\,$
Solution 2
We'll unfold the telescoping sum:
$\displaystyle \begin{align} \sum_{k=1}^nk^2(k+1)! &=\sum_{k=1}^n\left[(k+2)^2-4(k+1)\right](k+1)!\\ &=\sum_{k=1}^n[(k+2)(k+2)!-4(k+1)(k+1)!]\\ &=\sum_{k=1}^n[(k+3-1)(k+2)!-4(k+2-1)(k+1)!]\\ &=\sum_{k=1}^n[(k+3)!-(k+2)!-4(k+2)!+4(k+1)!]\\ &=\sum_{k=1}^n[(k+3)!-5(k+2)!+4(k+1)!]\\ &=\sum_{k=4}^{n+3}k!-5\sum_{k=3}^{n+2}k!+4\sum_{k=2}^{n+1}k!\\ &=(n+3)!-4(n+2)!+2 = (n+2)!(n-1)+2. \end{align}$
Thus the equation reduces to $(n+2)(n-1)=108\,$ from which $n=10.$
Solution 3
Let
$\displaystyle S_k=\frac{1^2 2! + 2^2 3! + ... + k^2 (k+1)! -2}{(k+1)!}.$
We can rule out $n=1,2$ as solutions by observation. Thus, we are guaranteed to have an $S_2$ and an $S_3$ and verify that both are integers. In general, for some $k\geq3$,
$\displaystyle \begin{align}(k+1)!S_k-k!S_{k-1}&=k^2(k+1)! \\ \Rightarrow (k+1)S_k-S_{k-1}&=k^2(k+1) \end{align}$
By observing this equation, we claim that $S_k$ is a quadratic polynomial in $k$. Let $S_k=ak^2+bk+c$. Plugging this expression back into the recurrence relation and evaluating the undetermined coefficients,
$\displaystyle \begin{align}(k+1)(ak^2+bk+c)-[a(k-1)^2+b(k-1)+c]&=k^3+k^2 \\ ak^3+bk^2+(2a+c)k+(b-a)&=k^3+k^2 \end{align}$
Thus, $a=1$, $b=1$, $c=-2$ and $S_k=k^2+k-2$.
So, the equation becomes $S_n=n^2+n-2=108$. The two roots are $n=10$ and $n=-11$. Thus, the only permissible solution in natural numbers is $n=10$.
Solution 4
Writing in Gamma functions, the LHS is $\displaystyle F(n)=\frac{\displaystyle -2+\sum_{k=1}^nk^2\Gamma(k+2)}{\Gamma(n+1)}.\,$ We have $\displaystyle \sum_{k=1}^nk^2\Gamma(k+2)=n\Gamma(n+3)-\Gamma(n+3)+2,\,$ and conclude
$\displaystyle F(n)=\frac{\Gamma(n+3)}{\Gamma(n+2)}(n-1)=(2+n)(n-1).$
Solving $(2+n)(n-1)=108,\,$ we get $n=10.$
Acknowledgment
Dan Sitaru has kindly posted at CutTheKnotMath facebook page a problem of his from the Romanian Mathematical Magazine and later sent me a LaTeX file with his solution (Solution 1). Solution 2 is by Kunihiko Chikaya; Solution 3 is by Amit Itagi; Solution 4 is by N. N. Taleb.
![]()
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73580254
