An Exercise in Complex Numbers: Problem 4217 from Crux
Problem
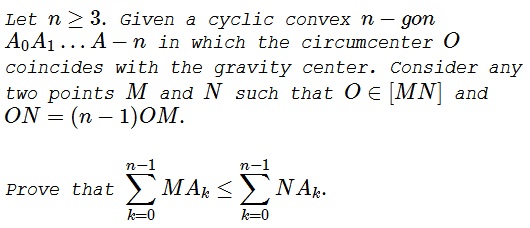
Solution
WLOG, assume that the $n-gon$ is inscribed into the unit circle centered at the origin. In the Argand plane, let $A_k=z_k,$ $|z_k|=1$ and, from the given condition $\displaystyle \sum_{k=0}^{n-1}z_k=0.$ Assume $M=-z$ and $N=(n-1)z,$ with $z$ an arbitrary complex number. The problem reduces to proving
$\displaystyle \sum_{k=0}^{n-1}|z+z_k|\le\sum_{k=0}^{n-1}|z_k-(n-1)z|.$
We have
$\displaystyle\begin{align}\sum_{m=0,m\ne k}^{n-1}|z_m-(n-1)z|&=\sum_{m=0,m\ne k}^{n-1}|\overline{z_m}||z_m-(n-1)z|\\ &=\sum_{m=0,m\ne k}^{n-1}|1-(n-1)z\overline{z_m}|\\ &\ge \left|\sum_{m=0,m\ne k}^{n-1}1-(n-1)\sum_{m=0,m\ne k}^{n-1}z\overline{z_m})\right|\\ &=\left|\sum_{m=0,m\ne k}^{n-1}(n-1)+(n-1)z\overline{z_k}\right|\\ &=(n-1)\left|1+z\overline{z_k}\right|\\ &=(n-1)|\overline{z_k}|\left|z_k+z\right|\\ &=(n-1)\left|z_k+z\right|\\ \end{align}$
It follows that
$\displaystyle \begin{align} \sum_{k=0}^{n-1}|1-(n-1)z\overline{z_k}|&=\frac{1}{n-1}\sum_{k=0}^{n-1}\left(\sum_{m=0,m\ne k}^{n-1}|1-(n-1)z\overline{z_m}|\right)\\ &\ge\sum_{k=0}^{n-1}|z+z_k|, \end{align}$
as required.
Acknowledgment
The problem is by Dan-Stefan Marinescu and Leonard Mihai Giugiuc, Romania. It appeared in the Canadian Crux Mathematicorum as #4217. No correct solutions were submitted and the magazine had eventually published the authors' solution. I am grateful to Leo Giugiuc for communicating to me the problem with the solution.
![]()
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73581049
