Arithmetic of Pie Sharing
Problem

Illustrations
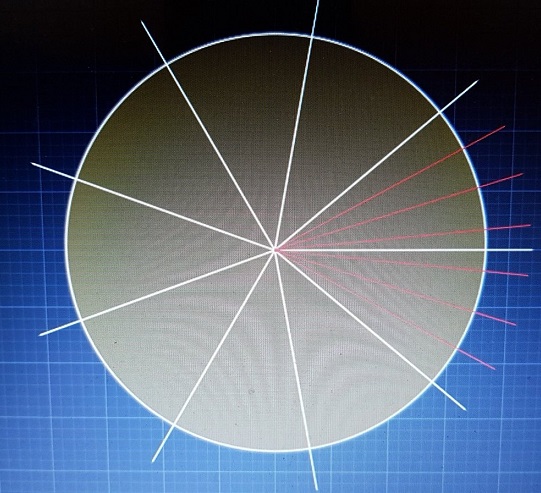
Below are several illustrations of $15=9+7-1$ cuts that solve the first part of the problem.
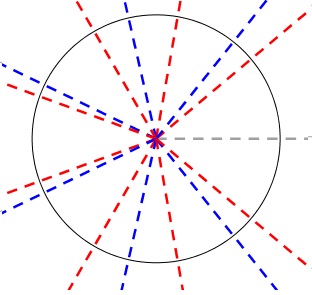
Thinking of a pie as a rectangle (Morth):
A different method altogether (Gökhan Karahan): Slice into 9 pieces first (white lines) than slice two pieces into 7 (red lines). Total cuts 15.
Solution
So assume the pie is cut into some pieces which could be combined into $1/p^{th}$ and (somehow else) into $1/q^{th}$ portions. Let's form a bipartite graph the following way: place $p$ nodes in one row and $q$ nodes in another row. These represent two groups of guests. Join two nodes (one in the upper row, the other in the low row) if in a combination of the cut-off pieces there is one piece both receive. Thus we get a graph where nodes represent guests and edges represent pieces of the pie.
We want to show that the number of edges (the pieces of the pie) is not less than $p+q-1.$ To this end note that among all graphs with a given number $N$ of nodes, the (spanning) trees have the smallest number of edges which is $N-1.$ Since in our case $N=p+q,$ $p+q-1$ is the smallest number of pieces with which it is possible to fairly satisfy either $p$ or $q$ guests.
Acknowledgment
This is problem M1232 (by D. Fomin) from the Russian magazine Kvant (1990, n7). The original solution is by A. Tolpygo and D. Fomin.
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73518529
