The Right Way to Write Numeral 4
The following has been published in
Mathematics Magazine, Vol. 75, No. 4, October 2002, p. 274
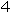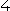 or  ? Mathematics or Accident?
ANA LUZÓN
MANUEL A. MORÓN
Depertmento de Matemática Aplicada a los Recursos Natureles
E. T. Superior de Ingenieros de Montes
Universidad Politécnica de Madrid
28040-Madrid, SPAIN
Readers may be unaware of the relationship between divisibility properties of numbers and topological properties of the numerals used to represent them. Let us use the word number for both the concept and the numeral. Given a number n, a proper prime divisor of n is a prime number, different from n, that divides n evenly. Note the following:
THEOREM. Consider the set of numbers S = {1, 2, 3, 4, 5, 6, 7, 8, 9}. For a, b ∈ S the following are equivalent:
a and b have the same number of proper prime divisors (counted with multiplicities).
a and b have the same homotopy type.
a and b cut a sheet in the same number of pieces if you write them down with a scalpel.
COROLLARY. A number in S (other than 1) is prime if and only if it has trivial homotopy type at equivalently, it does not tear the sheet in separate pieces.
We now answer the first question in our title:
COROLLARY. The correct symbol for the number four is , not .
Although the equivalence between (i) and (iii) in the theorem depends on Alexander-Pontryagin duality, this note, in spirit, belongs to the so called Shape Theory introduced by K. Borsuk. Readers may be interested to read Borsuk's book: Theory of Shape, Monografie Matematyczne, Polish Scientific Publishers, Warsaw, 1975.
Language of Mathematics, Language of Science and Plain Language
|Contact|
|Front page|
|Contents|
|Up|
|Store|
Copyright © 1996-2012 Alexander Bogomolny
| 
