Applications of Pick's Theorem

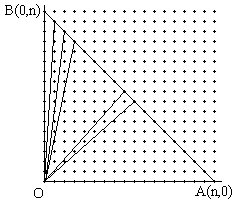
Problem 1

The line connecting two points A(n,0) and B(0,n) has a simple equation, x + y = n. Therefore, it contains all the points in the form (i, n - i), i an integer. There are n - 1 such points between A and B. Connect each one of them with the origin O. The lines divide ΔOAB into n small triangles.

Superimpose an integer grid on the diagram. The question is about the number of grid points that lie inside small triangles. Obviously, the two triangles next to the axes contain no grid points in their interiors. Prove that, for n prime, each of the remaining triangles contains exactly the same number of grid points.

Solution

Problem 2

An nxn square is randomly tossed onto an integer grid. Prove that it may never cover more than (n +1)² grid points.

Solution

References

R.Honsberger, Mathematical Morsels, MAA, 1978

Pick's Theorem
- Exercises for the Geoboard
- Pick's Theorem, A Proof
- Farey Series
- Pick's Theorem Applies to the Farey Series
- Stern-Brocot Tree
- Applications of Pick's Theorem

If n is prime then two numbers i and (n - i) are mutually prime for any i (the condition is both necessary and sufficient for the primality of n.) This means that the fraction i/(n - i) is irreducible or visible (from the origin.) We conclude that, besides the pieces OA and OB that run along the axes, no side of any of the small triangles contains a single grid point.

Now note that small triangles have the same base (1/n-th of AB) and the same height. Thus all of them share the same area. Since each of the triangles in question has exactly 3 grid points on its boundary (at its vertices), the conclusion follows immediate from Pick's theorem.

In case all four vertices of the square lie at grid points, the square contains (n-1)² grid points in its interior and 4n on its perimeter. Which totals exactly (n+1)² points. In a more general case, the perimeter of the square may only contain fewer than 4n points. Indeed, 1 is the smallest distance between the points on the grid. On a line (perimeter of the square) of length 4n there is simply no room for more than 4n points spaced at least 1 unit apart.

From Pick's theorem, n² = I - B/2 + 1, where I is the number of grid points in the interior of the square and B is the number of points on its boundary. The total number of points covered by the square is given by I + B:

I + B = I + B/2 - 1 + B/2 + 1 = n² + B/2 + 1≤ n² + 4n/2 + 1 = (n + 1)²

71547049