Draw a regular polygon, centered at the origin in the complex plane, with one comer being the number 1 (Figure 8.13). What are the complex numbers corresponding to all the comers? These numbers were studied by the English mathematician Abraham De Moivre (1667-1754) long before it was realized that they had a geometrical meaning.

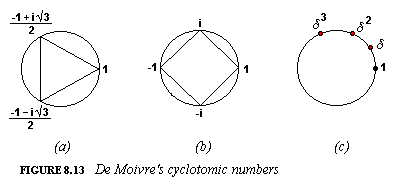
When the polygon is a square (Figure 8.13(b)), the answer is easy. The numbers (reading counterclockwise) are 1, i, - 1, -i. We call these the fourth-order De Moivre numbers. In a similar way, the third-order De Moivre numbers (Figure 8.13(a)) are 1, (-1+ i3)/2, 1 - i3)/2, and the sixth-order ones are these and their negatives:

(again reading counterclockwise). The fifth-order ones are a bit harder: You have to solve one quadratic equation on top of another.

What can we say about these numbers? They are all powers of one of them! The De Moivre number that immediately follows 1 in counterclockwise order we'll call _n (if the polygon has 1 coners), or just when 1 is obvious. Since the twirl that takes 1 to (Figure 8.13(c)) takes to ², ² to ³, and so on, we see that the full set of nth-order De Moivre numbers is

and we also see that ⁿ = 1. But we saw that ₄ = i, which satisfies ²+1=0, So ⁿ=1 is not always the simplest equation satisfied by _n. The following table gives the simplest equation for an for n = 1, . . . , 12.

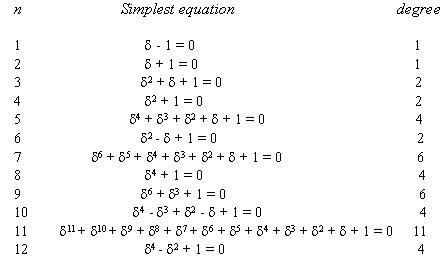
In fact, the nth-order De Moivre number, _n is an algebraic number whose degree is the nth of Euler's totient numbers, (n). The solutions of this equation are all the primitive nth roots of unity. They satisfy x^k=1 for k=n, but for no smaller values of k.

We said that ₅ could be found by solving one quadratic on top of another. In fact,

as you can see by writing the equation ⁴+³+²++1=0 in the form (²+/2+1)²=(5)²/4.

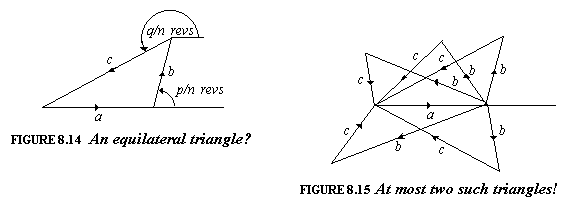
Suppose you have a triangle all of whose sides are rational numbers and all of whose angles are rational numbers of degrees. Then it must be equilateral! You might think that this was a very deep result, but in fact it's surprisingly easy to verify it, using De Moivre's numbers. Put your triangle in the complex plane (Figure 8.14). Then the angles indicated will be p nths and q nths of a revolution, where we take the smallest possible value of n. Since the three indicated shifts add up to zero, we see that the nth-order De Moivre number = _n must satisfy

as, therefore, must all the algebraic conjugates of _n that have the form ^k whenever k and n have no common factor.

So indeed we have (n) equations

and so (n) different triangles, such as in Figure 8.15, all of which have the same base and the same edge lengths, but different angles. This is nonsense, because there can be at most two such triangles: the original one (Figure 8.14) and its reflection in the base (the two rightmost in Figure 8.15). Now the only numbers with (n) 2 are n=1,2,3,4, or 6, so all angles are at least 1/6 of a revolution (i.e., 60^o), and your triangle must be equilateral, since its angles add up to 180^o.