Matrices Help Relationships
An Airline Problem

William A. McWorter Jr.

Consider the following problem.

Given n cities, it is desired to design a network of flights between the cities satisfying the following conditions. For each city there are direct flights to and from exactly the same number of other cities. Between any two cities there is exactly one flight with at most one stopover. For what values of n do such networks exist?

For n = 2, a solution is easy, one direct flight between the two cities. For n = 3 and 4 no network exists satisfying the required conditions. For n = 5, the graph below is one solution.

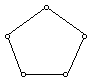
Let k denote the number of flights to and from a city. Here k = 2. For any one city, there are direct flights to and from exactly 2 cities, and between any two cities, there is exactly one flight with at most one stopover: a direct flight or a one-stopover flight, not both.

There are no such networks for n = 6, 7, 8, and 9 cities, as we shall show. However, for n = 10 there is a solution which is realized by the so-called Petersen graph.

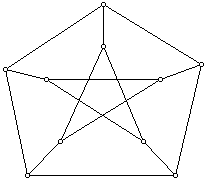
Again, you can check that all the conditions are satisfied. This graph has a high degree of symmetry (120 symmetries). It suffices to check the conditions for any one of the cities because of this symmetry. (To recognize the many symmetries of this graph, note that the same graph arises by taking as vertices all 2-element subsets of {1, 2, 3, 4, 5} and joining two such subsets by an edge if and only if they are disjoint)

With matrix theory we will show that there are only a small number of values for n for which there exists a network of flights between n cities satisfying the given conditions. Let A be the incidence matrix for the relationship "there is a direct flight between", with the rows and columns of A labelled by the cities. There is a 1 in a row labelled c and column labelled d if and only if there is a direct flight between c and d, zeros elsewhere. Then A is an n by n matrix of ones and zeros with the property that each row and column of A contains exactly k ones.

The integer powers of a square incidence matrix have a nice property in the context of networks. The entry in the i-th row, j-th column of A^d is the number of paths of length d from city i to city j. I haven't defined path in a network, but let's look at the solution for n = 5 cities.

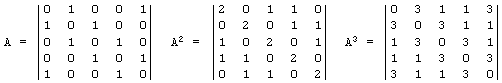
A path is what you'd expect a path to be, the path followed by an airplane in this network. The length of the path is the number of stops. For example, the entry in row 1, column 1 of A² is a 2, meaning that there are exactly two paths from city 2 to itself stopping somewhere else and finally stopping at city 2. These are 1 to 2 then 2 to 1 and 1 to 5 then 5 to 1. The entry in row 2, column 1 of A³ is 3, meaning that there are three paths from city 2 to city 1, namely, 2 to 1, 1 to 2, 2 to 1; 2 to 1, 1 to 5, 5 to 1; and 2 to 3, 3 to 2, 2 to 1. You may notice that it is easier to count these paths by multiplying matrices than counting the number of paths directly.

Now let's look at A² in the general case of n cities, assuming the network exists for n cities. The condition that there are direct flights to exactly k other cities implies that the main diagonal entries of A² are all equal to k. The condition that between any two cities there is exactly one flight with at most one stopover means that the off-diagonal entries of A² are either 0 because there is a direct flight between the two cities, or 1 because there is a one-stopover flight between the two cities (look at the example A² above for n = 5). The entries of matrix A hold the number of paths of length 1 between two cities. Hence the off-diagonal entries of A have a 1 where A² has a zero and vice versa (again, look at the example above). Further, the main diagonal entries of A are all zero. Thus we can write

A² + A - (k - 1)I = J

where I is the n by n identity matrix and J is the matrix of all ones.

Now we can take advantage of the concept of eigenvalues and eigenvectors of a square matrix. A nonzero vector v is an eigenvector of a square matrix M if Mv = λv, for some number λ. The number λ is called an eigenvalue and may be any number, including zero. Finding all the eigenvalues of a square matrix usually involves finding a determinant, but we won't need to do that here. Since all the row sums of A equal k, the vector v = (1, 1, ...) is an eigenvector of A:

Av = kv (therefore, A^dv = k^dv, for every positive integer d)

Thus,

nv = Jv = (A² + A - (k - 1)I)v = A²v + Av - (k - 1)v = (k² + k - (k - 1))v = (k² + 1)v.

Since v is not the zero vector, it follows that n = k² + 1, the number of cities has to be one more than a perfect square. That explains why n cannot be 3, 4, 6, 7, 8, or 9.

Now let u be any eigenvector of A with corresponding eigenvalue λ. Then Au = λu and

Ju = (A² + A - (k - 1)I)u = (λ² + λ - (k - 1))u.

Thus u is an eigenvector of J with eigenvalue λ² + λ - (k - 1). The matrix J is a very simple matrix so we know what its eigenvalues are, namely 0 n-1 times and n once. An n by n matrix has exactly n eigenvalues, counting repeats. For reasons too technical to outline here, the vector v = (1, 1, 1, ...) and its nonzero scalar multiples are the only eigenvectors of J associated with the eigenvalue n of J. Hence the remaining n-1 eigenvalues of A must satisfy the equation λ² + λ - (k - 1) = 0. Thus there are s eigenvalues of A equal to (-1 + √4k - 3)/2 and t eigenvalues of A equal to (-1 - √4k - 3)/2, with s + t = n - 1 = k².

We're almost there. The sum of all the eigenvalues of A must equal the sum of the diagonal entries of A, which sum is 0. Hence

k + s(-1 + √4k - 3)/2 + t(-1 - √4k - 3)/2 = 0, or
(s - t)√4k - 3 = s + t - 2k = k² - 2k.

Separate between two cases: s = t and s ≠ t. If s = t, k² - 2k = 0, so k = 0 or 2.

If s ≠ t, 4k - 3 is a complete square that divides the integer (k²-2k)². There are only finitely many such k. Since (k²-2k)² is congruent to 0 modulo 4k - 3, so is 4⁴(k²-2k)² = ((4k)²-2(4)(4k))². Since 4k is congruent to 3 modulo 4k - 3, it follows that (3²-2(4)(3))² = 225 is congruent to 0 modulo 4k - 3. The positive values of k such that 4k - 3 divides 225 are 1, 2, 3, 7, 12, and 57, making the only possibilites for n just 2, 5, 10, 50, 145, and 3250. We've seen examples for n = 2, 5, and 10. It turns out that there is an example for n = 50 and Michael Aschbacher has shown that there is no example for n = 3250. Since, for k = 12, 4k - 3 = 45 is not a complete square, n = 145 cannot occur either.

References

1. M. Aschbacher, The non-existence of rank three permutation groups of degree 3250 and subdegree 57, J. Algebra, 19 (1971), 538-540.

Related material Read more...
	Matrices Help Relationships
	Addition of Vectors and Matrices
	Multiplication of a Vector by a Matrix
	Multiplication of Matrices
	Matrix Groups
	Eigenvectors by Inspection
	Vandermonde matrix and determinant
	When the Counting Gets Tough, the Tough Count on Mathematics
	Merlin's Magic Squares

|Contact| |Front page| |Contents| |Algebra|

Copyright © 1996-2018 Alexander Bogomolny