Cyclic Quadrilateral from the USAMO
Xiaoxue Li
Am Math Monthly, V 123, N 1, Jan 2016, p. 96
Here is problem 2, Part I, of the 28th United States of America Mathematical Olympiad.
Let $ABCD\;$ be a cyclic quadrilateral.
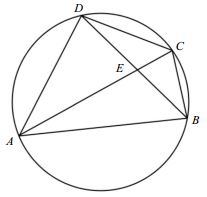
Prove that
$|AB-CD+|AD-BC|\ge 2|AC-BD|.$
Solution
It may be assumed without loss of generality that $AB\ge CD,\;$ $AD\ge BC,\;$ and $AC\ge BD.\;$ It then suffices to show that $(AB-CD)+(AD-BC)\ge 2(AC-BD).\;$ We introduce auxiliary points $A',\;$ $C',\;$ and $D'\;$ such that $EC-EC',\;$ $ED=ED',\;$ and $AA'=CD.\;$ Observe that triangles $CDE\;$ and $C'D'E\;$ are congruent.
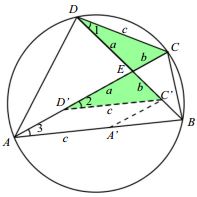
$\angle 1=\angle 3=\angle 2,\;$ implying that $C'D'\parallel AB.\;$ By the construction $\Delta EC'D'=\Delta ECD,\;$ in particular, $C'D'=CD=AA',\;$ making AD'C'A' a parallelogram. Thus, $AB-CD=A'B.\;$ Also
$\begin{align} AC-BD &= AC-(a+b+BC')\\ &=AD'-BC'\\ &=A'C'-BC'\\ &\le A'B. \end{align}$
It follows that $AB-CD\ge AC-BD.\;$ Similarly, $AD-BC\ge AC-BD.\;$ Adding these two inequalities yields the desired inequality. Equality holds when $ABCD\;$ is a rectangle.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73578498
