Three Dimensional Cross
H. Shutrick
15 July, 2009
A useful exercise for students learning multiple integrals is to calculate the volume of wood that remains from a cube with edge of length 2 when holes of diameter 1 have been bored from the centre of each face to the centre of the opposite face.
One way of solving it is to use the formula for the measure of the union of three sets: if the three cylinders that have been removed are X, Y and Z, then the volume of their union is
|X ∪ Y ∪ Z| = |X| + |Y| + |Z| - |X ∩ Y| - |Y ∩ Z| - |Z ∩ Z| + |X ∩ Y ∩ Z|
Clearly |X| = |Y| = |Z| = 2π(1/2)².
If the coordinate axes are the axes of the cylinders, then the part of
Moreover, the upper part of X ∩ Y ∩ Z is the inside of the tent that is above the circle of diameter 1 centred at the origin.
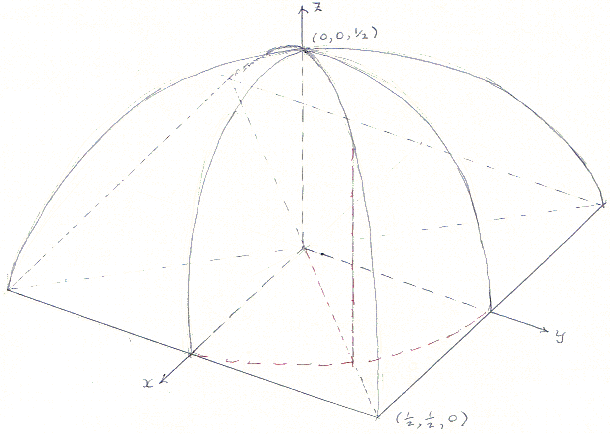
If you calculate the integrals involved, you may be surprised to discover that the formula for the volume is quite simple, but my practical colleague, Thomas Martinsson, pointed out that the three dimensional cross formed by the cylinders can be made from 24 pieces of quarter round beading of length 1 and radius 1/2 if you slice off a certain section from each of them.
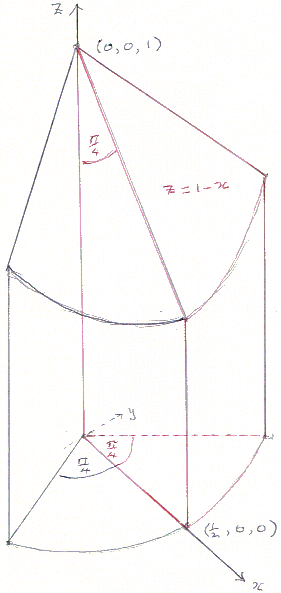
In the diagram, the z-axis is the axis of the beading and the xz-plane is its plane of symmetry. Its volume is then
D = {(r, θ): 0 ≤ r ≤ 1/2, 0 ≤ θ ≤ π/4}.
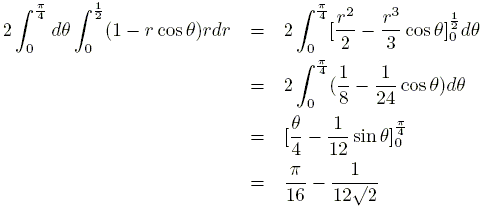
The volume of wood remaining is 8 - 24(π/16 - 1/12√2) = 8 - 3π/2 + √2.
The formula for the measure of the union of three sets is relevant, but again unnecessary, for the famous problem of the hotly fought battle between 100 pensioners round the Christmas buffet where 80 of them lost a tooth, 70 of them lost an eye and 60 of them lost an ear. Find how many, at least, lost all three.
(This article is also available as a pdf file.)
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73563789
