Number Guessing
In this simple game, your computer does all the work. You only have to press one of the buttons, "Yes" or "No". This is how you play. At the beginning (or after pressing "Reset"), you think of a positive integer less than 100. At any time, the computer will display a set of numbers. In response, press either "Yes" or "No" depending on whether your number is on the screen or not. After a while the computer will guess your number. See for yourself.
| What if applet does not run? |
The game's magical powers have a very simple explanation. Computer displays seven sets of numbers. For every i from 0 to 6, it displays the numbers with the same (either 0 or 1, selected randomly) binary digit in the i-th position counting from right. Answering "Yes" you actually tell your computer whether the digit is 0 or 1. Thus digit after digit, your computer collects the information about the binary representation of the number you thought up. Since (1111111)2 = 127 > 100, any number below 100 needs at most 7 bits to be written in the binary system.
For example, assume you selected 54. Its binary representation is 110110. I have to guess 6 binary digits. All numbers split into two groups: those that have the rightmost digit 0 and the rest that have the rightmost digit 1. 54 belongs to the first group. I randomly select which group (below 100) to display. Your answer will be either "Yes" or "No", depending on which of the two groups actually shows up. But, regardless of which group is shown, once you press one of the buttons, I shall determine the rightmost digit of your number. With 54 in mind, if you see the first group, you will press the "Yes" button. If you see the second group, your response will be "No".
Other digits are determined in the exactly same manner. Say, all numbers split into two groups: those that have their 3rd (from the right) digit equal to 0 (1, 2, 3, 8, 9, 10, 11, 16, 17, ...) and the rest that have 1 in the 3rd position (4, 5, 6, 7, 12, 13, 14, 15, 20, ...). I select one of the groups randomly. Your answer will depend on which of the two groups has been selected. But regradless, pressing one of the buttons you tell me which digit it is. For 54, if I display the first group, the answer must be "No". For the second group, the answer must be "Yes." In both cases I am given a means to realize that the 3rd digit of your number is 1.
Here's one screen shot.
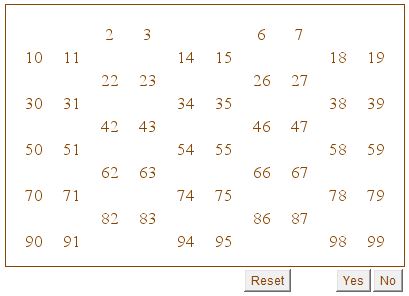
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1966-2016 Alexander Bogomolny
73587965
